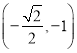Question

【题目】下列四个结论：

①命题“”的否定是“”；

②若是真命题，则可能是真命题；

③“且”是“”的充要条件；

④当时，幂函数在区间上单调递减.

其中正确的是

A. ①③ B. ②④ C. ①④ D. ②③

Answer 1

【答案】C

【解析】

①根据特称命题的否定方法进行判断;

②根据复合命题真假关系进行判断;

③根据充分条件和必要条件的定义进行判断;

④根据幂函数单调性进行判断.

①根据对特（全）称命题进行否定的方法是：改量词，否结论，命题“x0∈R，＜1”的否定是“”，故①正确；

②若p∧q是真命题，则p，q都是真命题，则￢p一定是假命题，故②错误；

③当a＞5且b＞-5时，则a+b＞0，即充分性成立，

当a=2，b=1时，满足a+b＞0，但a＞5且b＞-5不成立，即“a＞5且b＞-5”是“a+b＞0”的充分不必要条件，故③错误；

④根据幂函数单调性，当a＜0时，幂函数y=xa在区间（0，+∞）上单调递减．故④正确，

故选C