题目内容
已知函数 .
.
(1) 当 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值;
(2) 若 在
在 上是单调函数,求实数a的取值范围.
上是单调函数,求实数a的取值范围.
【解析】本试题考查了导数在研究函数中的运用。利用导数判定函数的单调性和求解函数的极值,以及运用逆向思维,求解参数取值范围的问题。
【答案】
(1) 易知,函数 的定义域为
的定义域为 .
.
当 时,
时, .
.
当x变化时, 和
和 的值的变化情况如下表:
的值的变化情况如下表:
|
x |
(0,1) |
1 |
(1,+∞) |
|
|
- |
0 |
+ |
|
|
递减 |
极小值 |
递增 |
由上表可知,函数 的单调递减区间是(0,1)、单调递增区间是(1,+∞)、
的单调递减区间是(0,1)、单调递增区间是(1,+∞)、
极小值是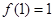 ( 5 分 )
( 5 分 )
(2) 由 ,得
,得 .
.
①若函数 为
为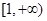 上单调增函数, 则
上单调增函数, 则 在
在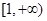 上恒成立,即不等式
上恒成立,即不等式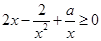 在
在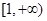 上恒成立. 也即
上恒成立. 也即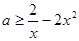 在
在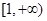 上恒成立.又
上恒成立.又 在
在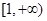 上为减函数,
上为减函数,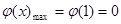 . 所以
. 所以 .
.
② 若函数 为
为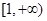 上单调减函数, 则
上单调减函数, 则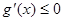 在
在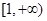 上恒成立,即
上恒成立,即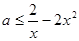 在
在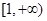 上恒成立.又
上恒成立.又 在
在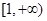 上为减函数,
上为减函数,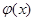 不存在最小值. 所以
不存在最小值. 所以 不成立.
不成立.
综上 

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目