题目内容
下面四个说法中,正确的个数为( )
①三点确定一个平面;
②△ABC在平面α外,其三边延长线分别和α交于P,Q,R,则P,Q,R一定共线;
③一个角的两边所在直线分别平行于另一个角的两边所在直线,则这两角相等;
④在三维空间中,三个平面最多把空间分成八部分.
①三点确定一个平面;
②△ABC在平面α外,其三边延长线分别和α交于P,Q,R,则P,Q,R一定共线;
③一个角的两边所在直线分别平行于另一个角的两边所在直线,则这两角相等;
④在三维空间中,三个平面最多把空间分成八部分.
分析:①不共线的三点确定一个平面;
②根据公理2可知结论正确;
③一个角的两边所在直线分别平行于另一个角的两边所在直线,则这两角相等或互补;
④在三维空间中,三个平面把空间分成四、六、七、八部分.
②根据公理2可知结论正确;
③一个角的两边所在直线分别平行于另一个角的两边所在直线,则这两角相等或互补;
④在三维空间中,三个平面把空间分成四、六、七、八部分.
解答:解:①不共线的三点确定一个平面,故①不正确;
②根据公理2,△ABC在平面α外,其三边延长线分别和α交于P,Q,R,则P,Q,R一定共线,故②正确;
③一个角的两边所在直线分别平行于另一个角的两边所在直线,则这两角相等或互补,故③不正确;
④在三维空间中,三个平面最多把空间分成八部分,正确,如图所示,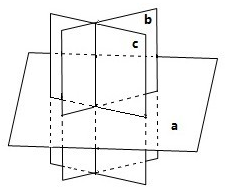
故选B.
②根据公理2,△ABC在平面α外,其三边延长线分别和α交于P,Q,R,则P,Q,R一定共线,故②正确;
③一个角的两边所在直线分别平行于另一个角的两边所在直线,则这两角相等或互补,故③不正确;
④在三维空间中,三个平面最多把空间分成八部分,正确,如图所示,

故选B.
点评:本题考查平面的基本性质及推论,考查两个平面相交只有一条交线,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目