题目内容
三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6个大题,共76分)。
17.(12分)以下资料是一位销售经理收集来的每年销售额和销售经验年数的关系:
| 销售经验(年) | 1 | 3 | 4 | 4 | 6 | 8 | 10 | 10 | 11 | 13 |
| 年销售额(千元) | 80 | 97 | 92 | 102 | 103 | 111 | 119 | 123 | 117 | 136 |
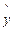 =78+4.2x,计算
=78+4.2x,计算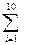 (yi-
(yi-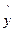 i)2;
i)2; (2)依据这些数据由最小二乘法求线性回归方程,并据此计算
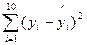 ;
;(3)比较(1)和(2)中的残差平方和
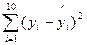 的大小.
的大小.
解:(1)散点图与直线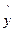 =78+4.2x的图形如下图,
=78+4.2x的图形如下图,
对x=1,3,…,13,有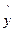 i=82.2,90.6,94.8,94.8,103.2,111.6,120,120,124.2,132.6,
i=82.2,90.6,94.8,94.8,103.2,111.6,120,120,124.2,132.6,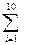 (yi-
(yi-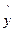 i)2=179.28.
i)2=179.28.
(2) =
=
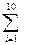 xi=7,
xi=7,
lxx= (xi-
(xi- )2=142,
)2=142, =108,
=108,
lxy=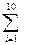 (xi-
(xi- )(yi-
)(yi- )=568,
)=568,
∴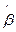 1=
1=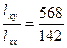 =4,
=4,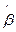 0=
0=  -
- 1=108-7×4
1=108-7×4
=80,故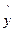 =80+4x.
=80+4x.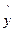 i=84,92,96,96,104,112,120,120,124,132,
i=84,92,96,96,104,112,120,120,124,132,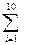 (yi-
(yi-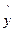 i)2=170.
i)2=170.
(3)比较可知,用最小二乘法求出的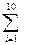 (yi-
(yi-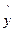 i)2较小
i)2较小
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本题12分)为了研究化肥对小麦产量的影响,某科学家将一片土地划分成200个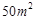 的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
表1:施用新化肥小麦产量频数分布表
| 小麦产量 | 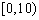 | 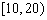 | 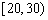 | 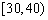 | 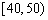 |
| 频数 | 10 | 35 | 40 | 10 | 5 |
| 小麦产量 | 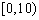 | 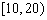 | 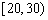 | 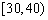 |
| 频数 | 15 | 50 | 30 | 5 |
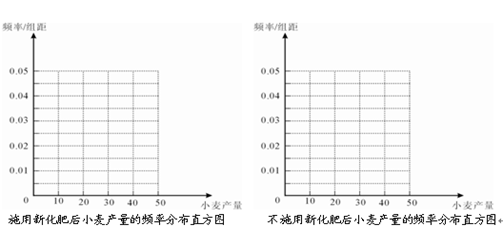
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计施用化肥和不施用化肥的一小块土地的小麦平均产量;
(3)完成下面2×2列联表,并回答能否有99.5%的把握认为“施用新化肥和不施用新化肥的小麦产量有差异”
表3:
| | 小麦产量小于20kg | 小麦产量不小于20kg | 合计 |
| 施用新化肥 | 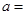 | 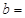 | |
| 不施用新化肥 | 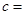 |  | |
| 合计 | | | 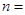 |
附:
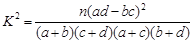
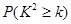 | 0.050 | 0.010 | 0.005 | 0.001 |
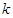 | 3.841 | 6.635 | 7.879 | 10.828 |

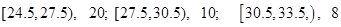
 名
名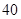 岁以上的人进行了调查,结果是:患胃病者生活不规律的共
岁以上的人进行了调查,结果是:患胃病者生活不规律的共 人,患胃病者生活规律的共
人,患胃病者生活规律的共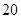 人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共
人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共 人.
人.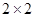 列联表.
列联表.
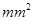 )
)

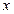 (万元)与销售额y(万元)之间有如下的对应数据
(万元)与销售额y(万元)之间有如下的对应数据 的值
的值 公式:
公式: 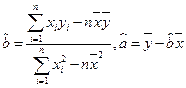 )
) 2
2
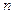 ;
;