Question

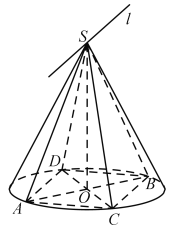
【题目】如图，已知圆锥的顶点为S，底面圆O的两条直径分别为和，且，若平面平面，以下四个结论中正确的是( )

A.平面

B.

C.若E是底面圆周上的动点，则的最大面积等于的面积

D.l与平面所成的角为45°

Answer 1

【答案】ABD

【解析】

利用直线与平面的性质判断直线与平面平行，直线与直线的平行，三角形的面积的最值的求法，直线与平面所成角判断选项的正误即可．

解：已知圆锥的顶点为，底面圆的两条直径分别为和，且，若平面平面，

所以是正方形．所以，平面，所以平面；正确；

因为，平面，，平面，平面，所以；正确；

若是底面圆周上的动点，当时，则的最大面积等于的面积；

当时，的最大面积等于两条母线的夹角为的截面三角形的面积，所以不正确；

因为，与平面所成的角就是与平面所成角，就是．所以正确；

故选：ABD．