题目内容
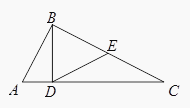
【题目】如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 和
和![]() 是全等的等腰梯形,其中
是全等的等腰梯形,其中![]() ,且
,且![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 是
是![]() 的中点.
的中点.

(I)请在图中所给的点中找出两个点,使得这两个点所在直线与平面![]() 垂直,并给出证明;
垂直,并给出证明;
(II)求二面角![]() 的余弦值;
的余弦值;
(III)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?如果存在,求出
?如果存在,求出![]() 的长度,如果不存在,请说明理由.
的长度,如果不存在,请说明理由.
【答案】(I)见解析;(II)![]() ;(III)见解析.
;(III)见解析.
【解析】试题分析: ![]() 法一:向量法,分别以边
法一:向量法,分别以边![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() ,
, ![]() ,
, ![]() 轴,给出相应点坐标,证明
轴,给出相应点坐标,证明![]() ,
, ![]() 法二:先证
法二:先证![]()
![]() 接着证明所以
接着证明所以![]()
![]() 平面
平面![]() 即
即![]() 最后证得结果(2)要求二面角的平面角的余弦值就先求得平面
最后证得结果(2)要求二面角的平面角的余弦值就先求得平面![]() 的法向量,利用公式即可算出结果(3)法一:借助向量假设存在,计算可得
的法向量,利用公式即可算出结果(3)法一:借助向量假设存在,计算可得![]() 矛盾,故不存在;法二:假设存在点
矛盾,故不存在;法二:假设存在点![]() ,证得平面
,证得平面![]() 平面
平面![]() ,即有
,即有![]() 为平行四边形,所以
为平行四边形,所以![]() ,矛盾
,矛盾
解析:法一:向量法
(I)![]() ,
, ![]() 点为所求的点.
点为所求的点.
证明如下:
因为四边形![]() 是等腰梯形,点
是等腰梯形,点![]() 为
为![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
又平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() =
= ![]() ,
,
所以![]()
![]() 平面
平面![]()
同理取![]() 的中点
的中点![]() ,则
,则![]()
![]() 平面
平面![]() .
.
分别以边![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() ,
, ![]() ,
, ![]() 轴,建立如图所示的空间直角坐标系.
轴,建立如图所示的空间直角坐标系.
由![]() ,得
,得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
, ![]() .
.
所以![]() ,
, ![]()
又![]() ,
,
所以![]() 平面
平面![]()
(II)由(I)知平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则
![]() 即
即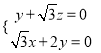
令![]() ,则
,则![]() ,
, ![]()
所以![]()
所以![]()
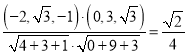
所以二面角![]() 的余弦值为
的余弦值为![]()
(III)假设存在点![]() ,使得
,使得![]()
![]() 平面
平面![]() .
.
设![]()
所以![]()
![]() ,所以
,所以![]()
而计算可得![]()
这与![]() 矛盾
矛盾
所以在线段![]() 上不存在点
上不存在点![]() ,使得
,使得![]()
![]() 平面
平面![]()
法二:(I)证明如下:
因为四边形![]() 是等腰梯形,点
是等腰梯形,点![]() 为
为![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,
的中点,
所以![]()
![]()
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]()
![]() 平面
平面![]()
因为![]()
![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,且
,且![]() ,
,
所以![]() 为菱形,所以
为菱形,所以![]()
因为![]() ,
,
所以![]() 平面
平面![]() .
.
(III)假设存在点![]() ,使得
,使得![]() 平面
平面![]()
由![]() ,所以
,所以![]() 为平行四边形,
为平行四边形,
所以![]()
因为![]() 平面
平面![]()
所以![]() 平面
平面![]()
又![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() 为平行四边形,所以
为平行四边形,所以![]() ,矛盾
,矛盾
所以不存在点![]() ,使得
,使得![]() 平面
平面![]()

【题目】海关对同时从![]() 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
地区 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进一步检测,求这2件商品来自相同地区的概率.