题目内容
20.任取x1、x2∈[a,b],且x1≠x2,若f($\frac{{x}_{1}+{x}_{2}}{2}$)>$\frac{f({x}_{1})+f({x}_{2})}{2}$,恒成立,则f(x)称为[a,b]上的凸函数.下列函数中①y=2x,②y=log2x,③y=x${\;}^{\frac{1}{2}}$在其定义域上为凸函数是( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
分析 由凸函数的概念,得出凸函数的几何特征,根据几何特征可作出四个函数①y=2x,②y=log2x,③y=x${\;}^{\frac{1}{2}}$的图象,观察图象即可得到答案.
解答  解:根据题意:任取x1,x2∈[a,b],且x1≠x2,若f($\frac{{x}_{1}+{x}_{2}}{2}$)>$\frac{f({x}_{1})+f({x}_{2})}{2}$,恒成立,f(x)称为[a,b]上的凸函数知:
解:根据题意:任取x1,x2∈[a,b],且x1≠x2,若f($\frac{{x}_{1}+{x}_{2}}{2}$)>$\frac{f({x}_{1})+f({x}_{2})}{2}$,恒成立,f(x)称为[a,b]上的凸函数知:
在函数y=f(x)的图象上任取不同的两点A、B,线段AB(端点除外)总在f(x)图象的上方,则函数f(x)为凸函数,
分别作出四个函数的图象,如图所示.
∴观察①y=2x,②y=log2x,③y=x${\;}^{\frac{1}{2}}$在其定义域上的图象,②,③满足凸函数的概念,
故选:B.
点评 本题考查函数的图象,关键在于作出符合凸函数的概念的函数图象,考查数形结合的思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列对应关系,不是数集M到数集N上的函数是( )
| A. | 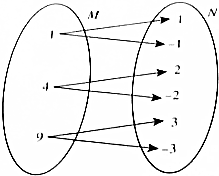 | B. | 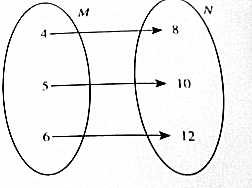 | ||
| C. | 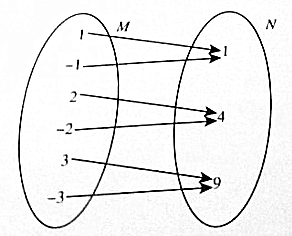 | D. | 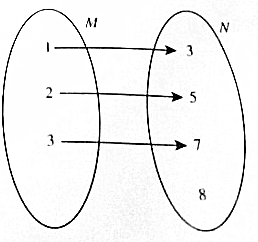 |
8.数列2,3,4,5,…的一个通项公式为( )
| A. | an=n | B. | an=n+1 | C. | an=n+2 | D. | an=2n |
15.已知向量$\vec a$与向量$\vec b$夹角为$\frac{π}{6}$,且$|\vec a|=\sqrt{3}$,$\vec a⊥(\vec a-2\vec b)$,则$|\vec b|$=( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 1 | D. | 2 |
12.三个数a=0.72,b=log20.7,c=20.7之间的大小关系是( )
| A. | a<c<b. | B. | a<b<c | C. | b<a<c | D. | b<c<a |
 已知函数f(x)=|x2-2x|.
已知函数f(x)=|x2-2x|.