题目内容
已知向量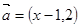 ,
,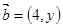 ,若
,若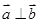 ,则
,则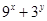 的最小值为 .
的最小值为 .
6
解析试题分析:因为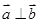 ,所以
,所以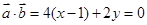 ,即
,即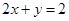 ,所以
,所以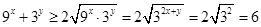 ,所以
,所以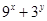 的最小值为6.
的最小值为6.
考点:向量的数量积
点评:主要是考查了向量垂直的坐标表示的运用,属于基础题。

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
题目内容
已知向量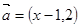 ,
,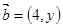 ,若
,若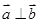 ,则
,则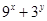 的最小值为 .
的最小值为 .
6
解析试题分析:因为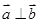 ,所以
,所以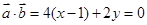 ,即
,即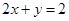 ,所以
,所以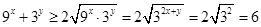 ,所以
,所以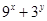 的最小值为6.
的最小值为6.
考点:向量的数量积
点评:主要是考查了向量垂直的坐标表示的运用,属于基础题。

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案