题目内容
设数列{an}是以2为首项,1为公差的等差数列,{bn}是以1为首项,2为公比的等比数列,则 =( )
=( )A.1033
B.1034
C.2057
D.2058
【答案】分析:首先根据数列{an}是以2为首项,1为公差的等差数列,{bn}是以1为首项,2为公比的等比数列,求出等差数列和等比数列的通项公式,然后根据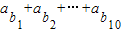 =1++2+23+25+…+29+10进行求和.
=1++2+23+25+…+29+10进行求和.
解答:解:∵数列{an}是以2为首项,1为公差的等差数列,
∴an=2+(n-1)×1=n+1,
∵{bn}是以1为首项,2为公比的等比数列,
∴bn=1×2n-1,
依题意有: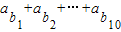 =1+2+22+23+25+…+29+10=1033,
=1+2+22+23+25+…+29+10=1033,
故选A.
点评:本题主要考查数列求和的知识点,解答本题的关键是要求出数列{an}和{bn}的通项公式,熟练掌握等比数列求和公式.
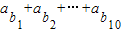 =1++2+23+25+…+29+10进行求和.
=1++2+23+25+…+29+10进行求和.解答:解:∵数列{an}是以2为首项,1为公差的等差数列,
∴an=2+(n-1)×1=n+1,
∵{bn}是以1为首项,2为公比的等比数列,
∴bn=1×2n-1,
依题意有:
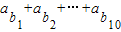 =1+2+22+23+25+…+29+10=1033,
=1+2+22+23+25+…+29+10=1033,故选A.
点评:本题主要考查数列求和的知识点,解答本题的关键是要求出数列{an}和{bn}的通项公式,熟练掌握等比数列求和公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设数列{an}是以2为首项,1为公差的等差数列,{bn}是以1为首项,2为公比的等比数列,则ab1+ab2+…+ab10=( )
| A、1033 | B、1034 | C、2057 | D、2058 |
设数列{an}是以2为首项,1为公差的等差数列,{bn}是以1为首项,2为公比的等比数列,则b a1+b a2+…+b a6等于( )
| A、78 | B、84 | C、124 | D、126 |
 =( )
=( )