题目内容
已知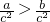
，则下列不等式一定成立的是
- A.a2＞b2
- B.lna＞lnb
- C.
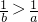
- D.
＞
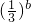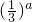
D
分析：利用条件，先判断出a＞b，对于A，B，C均不成立，可列举反例；对于D，利用函数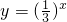
为R上的减函数，可得结论．
解答：由题意，∵c2＞0，，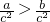
∴a＞b
若取a=1，b=-1，满足a＞b，但A，B，C均不成立．
∵函数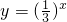为R上的减函数
∴
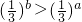，即D正确
故选D．
点评：本题考查的重点是不等式的基本性质，解题的关键是判断出a＞b，不成立列举反例．
分析：利用条件，先判断出a＞b，对于A，B，C均不成立，可列举反例；对于D，利用函数
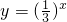为R上的减函数，可得结论．解答：由题意，∵c2＞0，
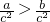，∴a＞b
若取a=1，b=-1，满足a＞b，但A，B，C均不成立．
∵函数
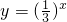为R上的减函数∴
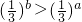，即D正确故选D．
点评：本题考查的重点是不等式的基本性质，解题的关键是判断出a＞b，不成立列举反例．
练习册系列答案
相关题目
若对可导函数f（x），g（x），当x∈[0，1]时恒有f′（x）•g（x）＜f（x）•g′（x），若已知α，β 是一锐角三角形的两个内角，且α≠β，记F′（x）=
(g(x)≠0)，则下列不等式正确的是（ ）
| f(x) |
| g(x) |
| A、F（sinα）＜F（cosβ） |
| B、F（sinα）＜F（sinβ） |
| C、F（cosα）＞F（cosβ） |
| D、F（cosα）＜F（cosβ） |
，则下列不等式成立的是 （ ）
B．
C．
D．
，则下列不等式成立的是 （ ）
B．
C．
D．