题目内容
设对于任意的实数x,y,函数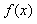 ,
,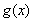 满足
满足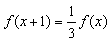 , 且f(0)=3,g(x+y)=g(x)+
, 且f(0)=3,g(x+y)=g(x)+
2y,g(5)=13,n∈N*。
(Ⅰ)求数列 和
和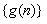 的通项公式;
的通项公式;
(Ⅱ)设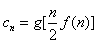 ,求数列
,求数列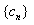 的前n项和Sn;
的前n项和Sn;
(Ⅲ)设F(n)=Sn-3n,存在整数m和M,使得对任意正整数n不等式m<F(n)<M恒成立,求M-m的最小值。
解:(Ⅰ)取x=n,得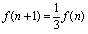 ,
,
取x=0,得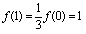 ,
,
故数列
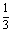
 ) n-1。
) n-1。
取x=n,y=1得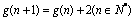 ,即
,即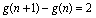 ,
,
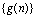
又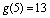 ,
,
所以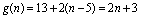 。
。
(Ⅱ) ,
,
∴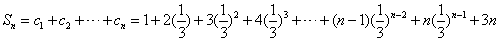 ,
,
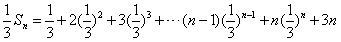 ,
,
两式相减,得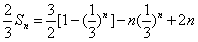 ,
,
∴ 。
。
(Ⅲ)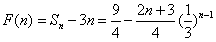 ,
,
∴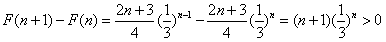 ,
,
所以F(n)
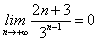 ,则
,则 ,
,
由于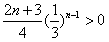 ,则
,则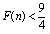 ,
,
所以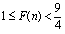 ,
,
因此当
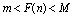
所以存在正数m=0,-1,-2
使得对任意的正整数n,不等式
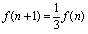 ,
,取x=0,得
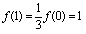 ,
,故数列

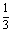
 ) n-1。
) n-1。取x=n,y=1得
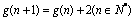 ,即
,即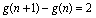 ,
,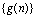
又
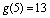 ,
,所以
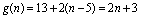 。
。(Ⅱ)
 ,
,∴
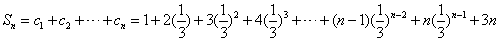 ,
,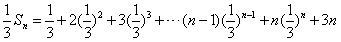 ,
,两式相减,得
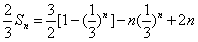 ,
,∴
 。
。(Ⅲ)
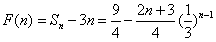 ,
,∴
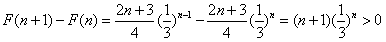 ,
,所以F(n)
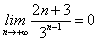 ,则
,则 ,
,由于
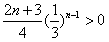 ,则
,则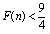 ,
,所以
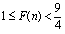 ,
,因此当

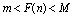
所以存在正数m=0,-1,-2
使得对任意的正整数n,不等式


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
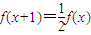 ,且f(0)=2,g(x+y)=g(x)+2y,g(3)=5,an=f(n),bn=g(n),n?N*. (Ⅰ)求数列an,bn的通项公式bn的通项公式
,且f(0)=2,g(x+y)=g(x)+2y,g(3)=5,an=f(n),bn=g(n),n?N*. (Ⅰ)求数列an,bn的通项公式bn的通项公式