题目内容
(8分)如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:

(1) FD∥平面ABC;
(2) AF⊥平面EDB.

(1) FD∥平面ABC;
(2) AF⊥平面EDB.
略


(1)取AB的中点M,连FM,MC,
∵ F、M分别是BE、BA的中点 ∴ FM∥EA, FM=
 EA
EA∵ EA、CD都垂直于平面ABC ∴ CD∥EA∴ CD∥FM
又DC="a, " ∴ FM="DC " ∴四边形FMCD是平行四边形
∴ FD∥MC…………………………………………………………………………4分
FD∥平面ABC
(2) 因M是AB的中点,△ABC是正三角形,所以CM⊥AB
又 CM⊥AE,所以CM⊥面EAB, CM⊥AF, FD⊥AF,
因F是BE的中点, EA=AB
所以AF⊥EB. ……………………………………8分


练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 的交点且垂直于直线
的交点且垂直于直线 的直线方程.
的直线方程. 射到直线
射到直线 上, 被
上, 被



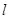 经过两条直线
经过两条直线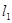 :
: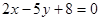 和
和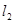
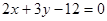 的交点,且分这两条直线与
的交点,且分这两条直线与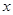 轴围成的三角形面积为
轴围成的三角形面积为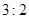 两部分,求直线
两部分,求直线 :
: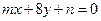 和
和 :
: ,
, ,求
,求 的值;
的值; ,试确定
,试确定 与L2:
与L2: 互相垂直,则
互相垂直,则 的值为______
的值为______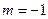 是直线
是直线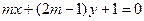 和直线
和直线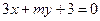 垂直的 ( )
垂直的 ( )