题目内容
9.已知向量$\vec a$,$\vec b$满足$\vec a$=$(-2sinx,\sqrt{3}(cosx+sinx))$,$\vec b$=(cosx,cosx-sinx),函数f(x)=$\vec a$•$\vec b$(x∈R).(Ⅰ)将f(x)化成Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的形式;
(Ⅱ)求函数f(x)的单调递减区间;
(Ⅲ) 求函数f(x)在$x∈[0,\frac{π}{2}]$的值域.
分析 (Ⅰ)根据平面向量的数量积与三角函数的恒等变换,求出f(x)并化简即可;
(Ⅱ)根据正弦函数的单调减区间,求出函数f(x)的单调减区间;
(Ⅲ)求出x∈[0,$\frac{π}{2}$]时,函数f(x)的取值范围即可.
解答 解:(Ⅰ)∵$\vec a$=$(-2sinx,\sqrt{3}(cosx+sinx))$,$\vec b$=(cosx,cosx-sinx),
∴f(x)=$\vec a$•$\vec b$
=-2sinxcosx+$\sqrt{3}$(cosx+sinx)(cosx-sinx)
=-sin2x+$\sqrt{3}$cos2x
=2(sin2xcos$\frac{2π}{3}$+cos2xsin$\frac{2π}{3}$)
=2sin(2x+$\frac{2π}{3}$);
(Ⅱ)令$\frac{π}{2}$+2kπ≤2x+$\frac{2π}{3}$≤$\frac{3π}{2}$+2kπ,k∈Z,
即-$\frac{π}{6}$+2kπ≤2x≤$\frac{5π}{6}$+2kπ,k∈Z,
∴-$\frac{π}{12}$+kπ≤x≤$\frac{5π}{12}$+kπ,k∈Z,
∴f(x)的单调减区间为$[kπ-\frac{π}{12},kπ+\frac{5π}{12}],k∈Z$;
(Ⅲ)当x∈[0,$\frac{π}{2}$]时,∴2x∈[0,π],
∴2x+$\frac{2π}{3}$∈[$\frac{2π}{3}$,$\frac{5π}{3}$],
∴sin(2x+$\frac{2π}{3}$)∈[-1,$\frac{\sqrt{3}}{2}$],
∴2sin(2x+$\frac{2π}{3}$)∈[-2,$\sqrt{3}$];
即f(x)的值域是$[-2,\sqrt{3}]$.
点评 本题考查了平面向量的数量积以及三角函数的图象与性质的应用问题,是基础题目.

| A. | 7 | B. | 1 | C. | log72 | D. | 0 |
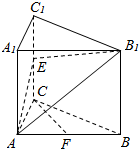 已知直棱柱ABC-A1B1C1,∠ACB=60°,AC=BC=4,AA1=6,E、F分别是棱CC1、AB的中点.
已知直棱柱ABC-A1B1C1,∠ACB=60°,AC=BC=4,AA1=6,E、F分别是棱CC1、AB的中点.