题目内容
若f（x）满足：
（1）定义域为R；
（2）f（x1+x2）=f（x1）f（x2）；
（3）f（1）=3；
（4）对任意x1＜x2，f（x1）＜f（x2）．
则函数f（x）的一个解析式为________．
解：根据题意，可取指数函数f（x）=3x
f（x）满足：
（1）定义域为R；
（2）f（x1+x2）=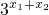
=
=f（x1）f（x2）；
（3）f（1）=31=3；
（4）对任意x1＜x2，f（x1）＜f（x2），即函数为增函数．
故答案为：f（x）=3x
分析：可取指数函数f（x）=3x，再验证满足所给的四个性质即可．
点评：本题考查函数模型的运用，考查函数的性质，掌握指数函数的性质是解题的关键．
f（x）满足：
（1）定义域为R；
（2）f（x1+x2）=
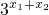==f（x1）f（x2）；（3）f（1）=31=3；
（4）对任意x1＜x2，f（x1）＜f（x2），即函数为增函数．
故答案为：f（x）=3x
分析：可取指数函数f（x）=3x，再验证满足所给的四个性质即可．
点评：本题考查函数模型的运用，考查函数的性质，掌握指数函数的性质是解题的关键．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
若f（x）满足f（-x）=f（x），且在（-∞，-1]上是增函数，则（ ）
A、f(-
| ||
B、f(-1)＜f(-
| ||
C、f(2)＜f(-1)＜f(-
| ||
D、f(2)＜f(-
|