题目内容
将函数f（x）=2sinx图象按向量
=（
，0）平移得函数g（x）的图象，则函数g（x）的单调递增区间是
- A.[2kπ-，2kπ+
]（k∈Z） - B.[2kπ-，2kπ+]（k∈Z）
- C.[2kπ+，2kπ+
]（k∈Z） - D.[2kπ+，2kπ+
]（k∈Z）
A
分析：直接利用左加右减的原则，求出平移后的函数解析式，然后结合基本函数的单调性求出函数的单调增区间．
解答：将函数f（x）=2sinx图象按向量=（，0）平移得函数g（x）=2sin（x-）的图象，
因为2k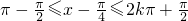
，k∈Z，
所以x∈[2kπ-，2kπ+]（k∈Z）．
所以函数的单调增区间为：[2kπ-，2kπ+]（k∈Z）．
故选A．
点评：本题是基础题，考查三角函数的图象的平移与伸缩变换，注意向量平移的方向，基本函数的单调性，考查计算能力．
分析：直接利用左加右减的原则，求出平移后的函数解析式，然后结合基本函数的单调性求出函数的单调增区间．
解答：将函数f（x）=2sinx图象按向量
=（，0）平移得函数g（x）=2sin（x-）的图象，因为2k
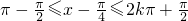，k∈Z，所以x∈[2kπ-
，2kπ+]（k∈Z）．所以函数的单调增区间为：[2kπ-
，2kπ+]（k∈Z）．故选A．
点评：本题是基础题，考查三角函数的图象的平移与伸缩变换，注意向量平移的方向，基本函数的单调性，考查计算能力．
练习册系列答案
相关题目
将函数f（x）=2sin（2x-θ）-3的图象F按向量
=(
，3)，平移得到图象F′，若F′的一条对称轴是直线x=
，则θ的一个可能取值是（ ）
| a |
| π |
| 6 |
| π |
| 4 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|