题目内容
已知抛物线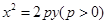 的焦点为
的焦点为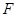 ,顶点为
,顶点为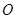 ,准线为
,准线为 ,过该抛物线上异于顶点
,过该抛物线上异于顶点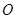 的任意一点
的任意一点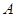 作
作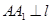 于点
于点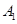 ,以线段
,以线段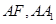 为邻边作平行四边形
为邻边作平行四边形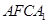 ,连接直线
,连接直线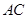 交
交 于点
于点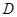 ,延长
,延长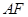 交抛物线于另一点
交抛物线于另一点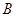 .若
.若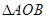 的面积为
的面积为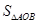 ,
,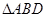 的面积为
的面积为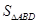 ,则
,则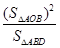 的最大值为____________.
的最大值为____________.

解析试题分析:如图,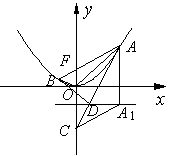
设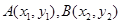 ,且设直线
,且设直线 的方程为
的方程为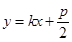 ,代入抛物线
,代入抛物线 方程,得
方程,得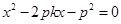 ,则
,则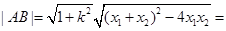
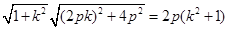 .因为点
.因为点 既在直线
既在直线 上,又在抛物线上,则
上,又在抛物线上,则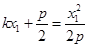 ,即
,即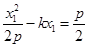 ①,由图易知
①,由图易知 ,
, ,则
,则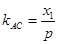 ,∴直线
,∴直线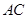 的方程为
的方程为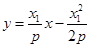 ,令
,令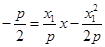 ,结合①,得
,结合①,得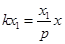 ,即
,即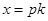 ,即点
,即点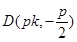 ,则点
,则点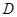 到直线
到直线 的距离
的距离 .又点
.又点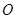 到直线
到直线 的距离
的距离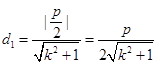 .又
.又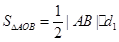 ,
,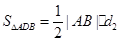 ,于是
,于是 =
=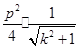 ,则当
,则当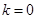 时,
时,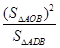 取得最大值
取得最大值 .
.
考点:1、抛物线几何性质;2、直线与抛物线的位置关系;3、点到直线的距离.

练习册系列答案
相关题目
 的离心率为
的离心率为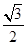 ,则双曲线
,则双曲线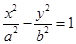 的渐近线方程是________
的渐近线方程是________ 与椭圆
与椭圆 的共同的左、右焦点,点P是两曲线的一个交点,且
的共同的左、右焦点,点P是两曲线的一个交点,且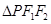 为等腰三角形,则该双曲线的渐近线方程是 。
为等腰三角形,则该双曲线的渐近线方程是 。 为坐标原点,
为坐标原点,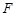 为抛物线
为抛物线 的焦点,
的焦点, 为抛物线
为抛物线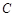 上一点,若
上一点,若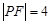 ,则
,则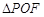 的面积为 .
的面积为 .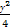 =1的交点为A,B,点P是椭圆上的动点,则使得△PAB的面积为
=1的交点为A,B,点P是椭圆上的动点,则使得△PAB的面积为 的点P的个数为 .
的点P的个数为 .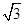 ,0),D(
,0),D( +y2=1上的动点,则
+y2=1上的动点,则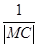 +
+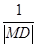 的最小值为________.
的最小值为________. =1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为________.
=1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为________. =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A,B两点.若AB的中点坐标为(1,-1),则E的方程为________.
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A,B两点.若AB的中点坐标为(1,-1),则E的方程为________. =1(a>b>0)上的一点A为圆心的圆与x轴相切于椭圆的一个焦点,与y轴相交于B、C两点,若△ABC是锐角三角形,则该椭圆的离心率的取值范围是________.
=1(a>b>0)上的一点A为圆心的圆与x轴相切于椭圆的一个焦点,与y轴相交于B、C两点,若△ABC是锐角三角形,则该椭圆的离心率的取值范围是________.