题目内容
设命题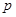 :实数x满足
:实数x满足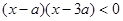 ,其中
,其中 ,命题
,命题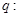 实数
实数 满足
满足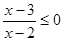 .
.
(Ⅰ)若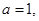 且
且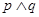 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(Ⅱ)若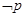 是
是
 的充分不必要条件,求实数
的充分不必要条件,求实数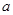 的取值范围.
的取值范围.
【答案】
(I)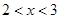 ;(III)
;(III)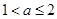 .
.
【解析】
试题分析:(I)解不等式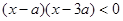 ,
,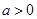 得命题
得命题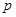 为真满足:
为真满足: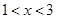 ;
;
解不等式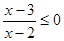 得命题
得命题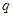 为真满足
为真满足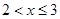 ;
;
为使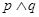 真,即
真,即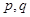 均为真命题,得到实数
均为真命题,得到实数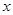 的取值范围
的取值范围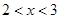 ;
;
(II)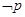 是
是
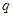 的充分不必要条件,即
的充分不必要条件,即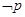 推出
推出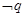 ,且
,且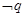 推不出
推不出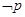 .
.
利用集合关系法,确定实数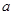 的不等式组.
的不等式组.
试题解析:(I)由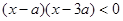 ,
,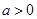 得,
得,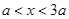 ,当
,当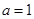 时,
时,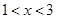 ,
,
即命题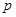 为真满足:
为真满足: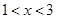 ;
;
由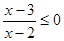 得
得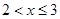 ,即命题
,即命题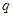 为真满足
为真满足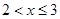 ;
;
若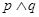 ,即
,即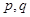 均为真命题,所以,实数
均为真命题,所以,实数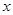 的取值范围
的取值范围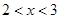 ;
;
(II)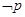 是
是
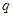 的充分不必要条件,即
的充分不必要条件,即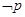 推出
推出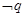 ,且
,且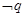 推不出
推不出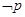 .
.
设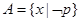 =
=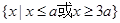 ,
,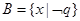 =
=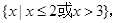 则
则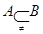 ,
,
所以,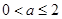 且
且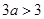 ,实数
,实数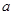 的取值范围
的取值范围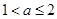 .
.
考点:简单逻辑联接词,真值表,简单不等式的解法.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
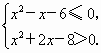
 ,
, q是
q是 p的必要不充分条件,求实数a的取值范围。
p的必要不充分条件,求实数a的取值范围。