题目内容
设数列{an}中的前n项和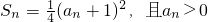 .
.
(1)求a1、a2;
(2)求{an}的通项.
解:(1)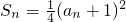
令n=1,可得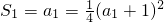 ,由a1>0,可得a1=1
,由a1>0,可得a1=1
令n=2,可得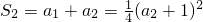 ,由a2>0,可得a2=3
,由a2>0,可得a2=3
(2)∵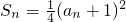
∴当n≥2时,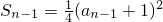
两式相减可得,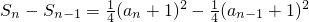
即4an=(an+1)2-(an-1-1)2
整理可得,(an-1)2=(an-1+1)2
∵an>0
∴an-1=an-1+1或an-1=-an-1-1(舍)
∴an-an-1=2
{an}是以1为首项,以2为公差的等差数列
∴an=1+(n-1)×2=2n-1
分析:(1)令n=1,利用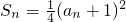 ,即可求出a1,在令n=2,即a1+a2=
,即可求出a1,在令n=2,即a1+a2= ,于是即可求出a2.
,于是即可求出a2.
(2)利用递推公式an=Sn-Sn-1,代入可求an
点评:本题主要考查了利用递推公式式an=Sn-Sn-1,求解数列的通项公式,解决此问题需要注意对n=1的检验,解决(2)主要是采用了构造特殊数列求解通项公式,要注意an>0的条件在解题中的应用.
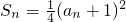
令n=1,可得
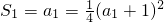 ,由a1>0,可得a1=1
,由a1>0,可得a1=1令n=2,可得
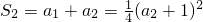 ,由a2>0,可得a2=3
,由a2>0,可得a2=3(2)∵
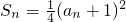
∴当n≥2时,
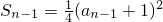
两式相减可得,
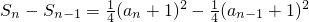
即4an=(an+1)2-(an-1-1)2
整理可得,(an-1)2=(an-1+1)2
∵an>0
∴an-1=an-1+1或an-1=-an-1-1(舍)
∴an-an-1=2
{an}是以1为首项,以2为公差的等差数列
∴an=1+(n-1)×2=2n-1
分析:(1)令n=1,利用
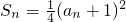 ,即可求出a1,在令n=2,即a1+a2=
,即可求出a1,在令n=2,即a1+a2= ,于是即可求出a2.
,于是即可求出a2.(2)利用递推公式an=Sn-Sn-1,代入可求an
点评:本题主要考查了利用递推公式式an=Sn-Sn-1,求解数列的通项公式,解决此问题需要注意对n=1的检验,解决(2)主要是采用了构造特殊数列求解通项公式,要注意an>0的条件在解题中的应用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
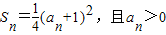 .
.