题目内容
在数列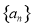 中,若存在非零整数
中,若存在非零整数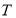 ,使得
,使得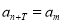 对于任意的正整数
对于任意的正整数 均成立,那么称数列
均成立,那么称数列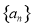 为周期数列,其中
为周期数列,其中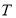 叫做数列
叫做数列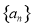 的周期,若数列
的周期,若数列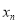 满足
满足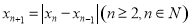 ,如
,如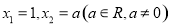 ,当数列
,当数列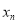 的周期最小时,该数列的前2015项的和是_____________.
的周期最小时,该数列的前2015项的和是_____________.
练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
题目内容
在数列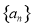 中,若存在非零整数
中,若存在非零整数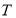 ,使得
,使得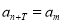 对于任意的正整数
对于任意的正整数 均成立,那么称数列
均成立,那么称数列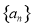 为周期数列,其中
为周期数列,其中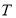 叫做数列
叫做数列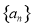 的周期,若数列
的周期,若数列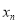 满足
满足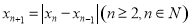 ,如
,如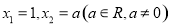 ,当数列
,当数列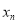 的周期最小时,该数列的前2015项的和是_____________.
的周期最小时,该数列的前2015项的和是_____________.
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案