题目内容
函数f(x)是定义域为R的可导函数,且对任意实数x都有f(x)=f(2-x)成立.若当x≠1时,不等式(x-1)•f′(x)<0成立,设a=f(0.5),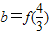 ,c=f(3),则a,b,c的大小关系是( )
,c=f(3),则a,b,c的大小关系是( )A.b>a>c
B.a>b>c
C.c>b>a
D.a>c>b
【答案】分析:由题意可得函数f(x)的图象关于直线x=1对称,f(x)在(0,+∞)上是减函数,在(-∞,0)上是增函数.再由|3-1|>|0.5-1|>| -1|,故 f(
-1|,故 f( )>f(0.5)>f(3),
)>f(0.5)>f(3),
由此得出结论.
解答:解:由f(x)=f(2-x)可得,函数f(x)的图象关于直线x=1对称.
再由 (x-1)•f′(x)<0成立可得,当x>1,f′(x)<0,故函数f(x)在(0,+∞)上是减函数;
当x<1,f′(x)>0,故函数f(x)在(-∞,0)上是增函数.
由于|3-1|>|0.5-1|>| -1|,故 f(
-1|,故 f( )>f(0.5)>f(3),即 b>a>c,
)>f(0.5)>f(3),即 b>a>c,
故选A.
点评:本题主要考查函数的对称性和单调性的应用,不等式与不等关系,属于基础题.
 -1|,故 f(
-1|,故 f( )>f(0.5)>f(3),
)>f(0.5)>f(3),由此得出结论.
解答:解:由f(x)=f(2-x)可得,函数f(x)的图象关于直线x=1对称.
再由 (x-1)•f′(x)<0成立可得,当x>1,f′(x)<0,故函数f(x)在(0,+∞)上是减函数;
当x<1,f′(x)>0,故函数f(x)在(-∞,0)上是增函数.
由于|3-1|>|0.5-1|>|
 -1|,故 f(
-1|,故 f( )>f(0.5)>f(3),即 b>a>c,
)>f(0.5)>f(3),即 b>a>c,故选A.
点评:本题主要考查函数的对称性和单调性的应用,不等式与不等关系,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目