题目内容
已知直角梯形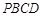 ,
,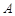 是
是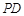 边上的中点(如图甲),
边上的中点(如图甲),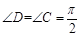 ,
,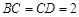 ,
,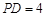 ,将
,将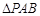 沿
沿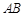 折到
折到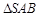 的位置,使
的位置,使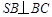 ,点
,点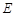 在
在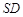 上,且
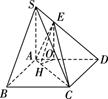
上,且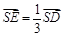 (如图乙)
(如图乙)
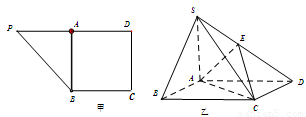
(Ⅰ)求证: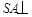 平面ABCD.
平面ABCD.
(Ⅱ)求二面角E−AC−D的余弦值
【答案】
(Ⅰ)见详解;(Ⅱ)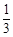
【解析】
试题分析:先证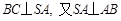 ,且
,且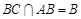 ,
,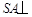 平面ABCD;根据几何法或向量法求出二面角E−AC−D的余弦值.
平面ABCD;根据几何法或向量法求出二面角E−AC−D的余弦值.
试题解析:
(Ⅰ)证明:在题图中,由题意可知,
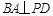 ,ABCD为正方形,所以在图中,
,ABCD为正方形,所以在图中,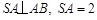 ,
,
四边形ABCD是边长为2的正方形,
因为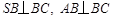 ,且
,且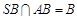 ,
,
所以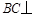 平面SAB,
(3分)
平面SAB,
(3分)
又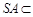 平面SAB,所以
平面SAB,所以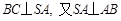 ,且
,且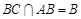 ,
,
所以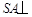 平面ABCD. (6分)
平面ABCD. (6分)
(Ⅱ)解:方法一: 如图,在AD上取一点O,使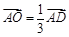 ,连接EO.
,连接EO.
因为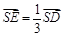 ,所以EO//SA ,
(7分)
,所以EO//SA ,
(7分)
所以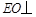 平面ABCD,过O作
平面ABCD,过O作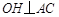 于H,连接EH,
于H,连接EH,
则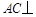 平面EOH,所以
平面EOH,所以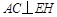 .
.
所以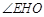 为二面角E−AC−D的平面角,
(9分)
为二面角E−AC−D的平面角,
(9分)
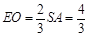 . 在Rt△AHO中,
. 在Rt△AHO中,
 .
(11分)
.
(11分)
所以二面角E−AC−D的余弦值为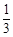 .
(12分)
.
(12分)
方法二:以A为原点建立空间直角坐标系,如图,
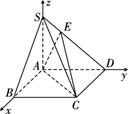
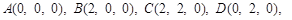
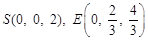 ,
(7分)
,
(7分)
易知平面ACD的法向量为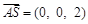 ,
,
设平面EAC的法向量为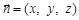 ,
,
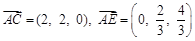 , (9分)
, (9分)
由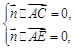 所以
所以 可取
可取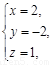
所以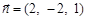 ,
(11分)
,
(11分)
所以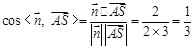 ,
,
所以二面角E−AC−D的余弦值为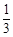 .
(12分)
.
(12分)
考点:线面垂直,二面角.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 已知直角梯形PBCD,A是PD边上的中点(如图3甲),
已知直角梯形PBCD,A是PD边上的中点(如图3甲),