题目内容
抛物线![]() 的准线的方程为
的准线的方程为![]() ,该抛物线上的每个点到准线
,该抛物线上的每个点到准线![]() 的距离都与到定点N的距离相等,圆N是以N为圆心,同时与直线
的距离都与到定点N的距离相等,圆N是以N为圆心,同时与直线![]() 和
和![]() 相切的圆.
相切的圆.
(1)求定点N的坐标; (2)是否存在一条直线![]() 同时满足下列条件:
同时满足下列条件:
① ![]() 分别与直线
分别与直线![]() 交于A、B两点,且AB中点为
交于A、B两点,且AB中点为![]() ;
;
② ![]() 被圆N截得的弦长为
被圆N截得的弦长为![]() .
.
解:(1)因为抛物线![]() 的准线的方程为
的准线的方程为![]()
所以![]() ,根据抛物线的定义可知:
,根据抛物线的定义可知:
点N是抛物线的焦点,
所以定点N的坐标为![]() ………………6分
………………6分
(2)
解:假设存在直线![]() 满足两个条件,显然
满足两个条件,显然![]() 斜率存在,
斜率存在,
设![]() 的方程为
的方程为![]() ,
,![]()
![]()
以N为圆心,同时与直线![]() 相切的圆N的
相切的圆N的
半径为![]() ,
,
因为![]() 被圆N截得的弦长为2,所以圆心到直线的距离等于1,
被圆N截得的弦长为2,所以圆心到直线的距离等于1,
即![]() ,
,
解得![]() ,
,
当![]() 时,显然不合AB中点为
时,显然不合AB中点为![]() 的条件,矛盾!
的条件,矛盾!
当![]() 时,
时,![]() 的方程为
的方程为![]()
由![]() ,
,
解得点A坐标为![]() ,
,
由![]() ,解得点B坐标为
,解得点B坐标为![]() ,
,
显然AB中点不是![]() ,矛盾!
,矛盾!
所以不存在满足条件的直线![]() . ………………14分
. ………………14分

练习册系列答案
相关题目
 的准线的方程为
的准线的方程为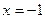 ,过点
,过点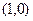 作倾斜角为
作倾斜角为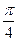 的直线
的直线 交该抛物线于两点
交该抛物线于两点 ,
, .求:(1)
.求:(1)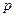 的值;(2)弦长
的值;(2)弦长
 的准线的方程为
的准线的方程为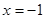 ,过点
,过点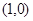 作倾斜角为
作倾斜角为 的直线
的直线 交该抛物线于两点
交该抛物线于两点 ,
, .求:(1)
.求:(1)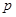 的值;(2)弦长
的值;(2)弦长