题目内容
已知函数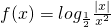 .
.
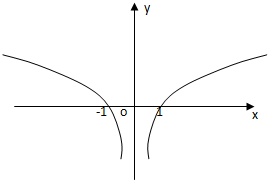
(1)请写出(不必证明)函数f(x)的定义域,奇偶性,单调性,值域,并画出图象;
(2)设任意的x1>0,x2>0,试猜测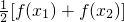 与
与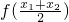 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
 解:(1)
解:(1)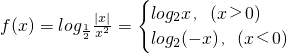
定义域:(-∞,0)∪(0,+∞);
奇偶性:偶函数;
单调性:函数
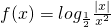
在区间(-∞,0)上为减函数;
在区间(0,+∞)上为增函数;
值域:(-∞,+∞);
图象如右:-------------(6分)
(2)对任意的x1>0,x2>0,
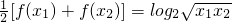 ,----------------(1分)
,----------------(1分)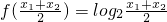 .-------------------------(1分)
.-------------------------(1分)因为
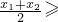
 ,当且仅当x1=x2时,等号成立,--------------------(2分)
,当且仅当x1=x2时,等号成立,--------------------(2分)由函数f(x)=log2x是单调递增函数,有
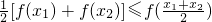 .
.当且仅当x1=x2时,等号成立.(此结论猜出得2分)------------------------(2分)
分析:(1)先作出函数图象,由函数解析式结合函数图象给出函数f(x)的定义域,奇偶性,单调性,值域;
(2)由题意可猜测
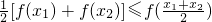 ,将此两代数式依据对数的运算性质化简,得到
,将此两代数式依据对数的运算性质化简,得到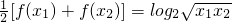 ,
,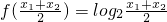 观察两式发现可用基本不等式比较两个真数的大小,从而证明出猜测的结论.
观察两式发现可用基本不等式比较两个真数的大小,从而证明出猜测的结论.点评:本题考查对数函数的图象与性质的综合应用,对数的运算性质,基本不等式比较大小,解题的关键是熟练掌握对数的性质及理解基本不等式,综合运用这些知识对猜测的结论进行证明

练习册系列答案
相关题目
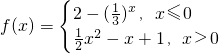 .
.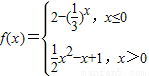 .
.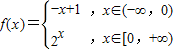 ,
,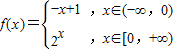 ,
,