题目内容
已知函数 的最小正周期为2π.
的最小正周期为2π.
(I)求ω的值;
(II)在△ABC中,角A、B、C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
解:(I)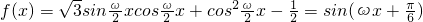 (4分)
(4分)
∵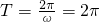 ∴ω=1∴
∴ω=1∴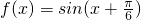 (6分)
(6分)
(II)∵(2a-c)cosB=bcosC∴2sinAcosB-sinCcosB=sinBcosC2sinAcosB=sin(B+C)=sinA
∴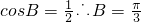 (8分)
(8分)
∵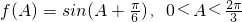 ∴
∴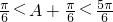 ∴
∴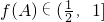 (10分)
(10分)
分析:(I)按多项式乘法化简函数,利用倍角公式化为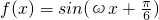 ,根据周期求ω的值;
,根据周期求ω的值;
(II)利用正弦定理化(2a-c)cosB=bcosC,为三角函数的关系,求出B的值,确定A的范围,再求函数f(A)的取值范围.
点评:本题考查y=Asin(ωx+φ)中参数的物理意义,三角函数的周期性及其求法,三角函数的最值,考查计算能力,分析问题解决问题的能力,是中档题.
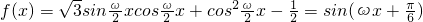 (4分)
(4分)∵
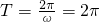 ∴ω=1∴
∴ω=1∴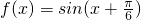 (6分)
(6分)(II)∵(2a-c)cosB=bcosC∴2sinAcosB-sinCcosB=sinBcosC2sinAcosB=sin(B+C)=sinA
∴
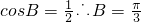 (8分)
(8分)∵
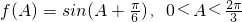 ∴
∴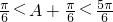 ∴
∴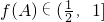 (10分)
(10分)分析:(I)按多项式乘法化简函数,利用倍角公式化为
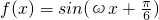 ,根据周期求ω的值;
,根据周期求ω的值;(II)利用正弦定理化(2a-c)cosB=bcosC,为三角函数的关系,求出B的值,确定A的范围,再求函数f(A)的取值范围.
点评:本题考查y=Asin(ωx+φ)中参数的物理意义,三角函数的周期性及其求法,三角函数的最值,考查计算能力,分析问题解决问题的能力,是中档题.

练习册系列答案
相关题目
 的最小正周期为
的最小正周期为 ,将其图象向左平移
,将其图象向左平移 个单位长度,所得图象关于
个单位长度,所得图象关于 轴对称,则
轴对称,则 的一个可能值是
( )
的一个可能值是
( ) B.
B. C.
C. D.
D.
 的最小正周期为2π.
的最小正周期为2π. ,求
,求 的值.
的值. 的最小正周期为π,其图象关于直线
的最小正周期为π,其图象关于直线 对称.
对称. 上的单调递增区间;
上的单调递增区间; 上只有一个实数解,求实数m的取值范围.
上只有一个实数解,求实数m的取值范围. 的最小正周期为
的最小正周期为 .
.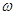 的值;
的值; 的最小正周期为
的最小正周期为
 的值;
的值;
 在
在
 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.