题目内容
设不等式组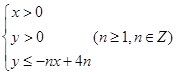 所表示的平面区域
所表示的平面区域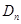 的整点个数为
的整点个数为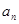 ,
,
则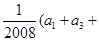
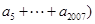 等于( )
等于( )
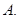
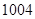
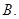
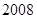
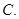
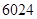
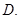
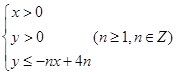 所表示的平面区域
所表示的平面区域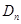 的整点个数为
的整点个数为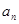 ,
,则
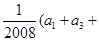
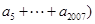 等于( )
等于( )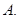
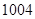
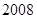
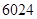
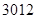
D
分析:利用不等式对应的图形为三角形,求出所有的整数点个数,判断出an为等差数列,利用等差数列的前n项和公式求出前n项和.
解答:解: (n∈N*)所表示的平面区域Dn的整点个数
(n∈N*)所表示的平面区域Dn的整点个数
an=3n+2n+n=6n
∴{an}为等差数列
∴a1,a3,…a2007也为等差数列
∴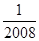 (a1+a3+…+a2007)
(a1+a3+…+a2007)
=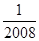 ×
× ═
═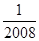 ×
×

=3012
故答案为D
解答:解:
 (n∈N*)所表示的平面区域Dn的整点个数
(n∈N*)所表示的平面区域Dn的整点个数an=3n+2n+n=6n
∴{an}为等差数列
∴a1,a3,…a2007也为等差数列
∴
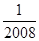 (a1+a3+…+a2007)
(a1+a3+…+a2007)=
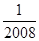 ×
× ═
═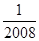 ×
×
=3012
故答案为D

练习册系列答案
相关题目
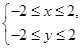 表示的区域为
表示的区域为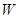 ,圆
,圆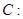
 及其内部区域记为
及其内部区域记为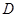 .若向区域
.若向区域


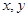 满足
满足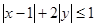 ,则由点
,则由点 构成的区域面积为( )
构成的区域面积为( )

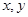 满足
满足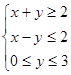 ,则
,则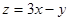 的取值范围是( )
的取值范围是( )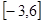

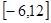
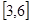
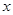 ,
,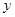 满足不等式组
满足不等式组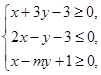 且
且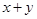 的最大值为9,则实数
的最大值为9,则实数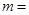 ( )
( )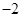 B
B 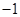 C 1 D 2
C 1 D 2 、
、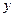 满足条件
满足条件 ,则
,则 的最小值是
的最小值是 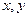 满足
满足 ,
, 、若
、若 ,求
,求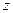 的最大值;
的最大值; 、若
、若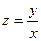 ,求
,求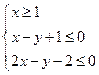 ,
,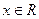 ,则
,则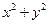 的最小值为
的最小值为