题目内容
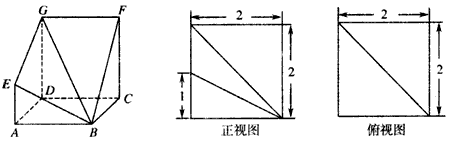
 如图,多面体ABCDEF中,平面ADEF⊥平面ABCD,正方形ADEF的边长为2,直角梯形ABCD中,AB∥CD,AD⊥DC,AB=2,CD=4.
如图,多面体ABCDEF中,平面ADEF⊥平面ABCD,正方形ADEF的边长为2,直角梯形ABCD中,AB∥CD,AD⊥DC,AB=2,CD=4.(Ⅰ)求证:BC⊥平面BDE;
(Ⅱ)试在平面CDE上确定点P,欲使点P到直线DC、DE的距离相等,且AP与平面BEF所成的角等于30°.
分析:(Ⅰ)欲证BC⊥平面BDE,根据直线与平面垂直的判定定理可知只需证BC与平面BDE内两相交直线垂直,根据面面垂直的性质可知ED⊥平面ABCD,则ED⊥BC,根据勾股定理可知BC⊥BD,满足定理所需条件;
(Ⅱ)DE,DA,DC两两垂直,以D为顶点,DA,DC,DE分别为x轴y轴z轴,建立直角坐标系D-xyz,求出D,A,E,B,F,以及
,
,设P(o,y,z)通过|y|=|z|.设
=(x′,y′,z′)是平面BEF的法向量,利用
,求出
,推出
与
所成的角为60°或120°.通过cos<
,
>=
和y|=|z|.求出P的坐标.
(Ⅱ)DE,DA,DC两两垂直,以D为顶点,DA,DC,DE分别为x轴y轴z轴,建立直角坐标系D-xyz,求出D,A,E,B,F,以及
| EF |
| EB |
| n |
|
| n |
| AP |
| n |
| AP |
| n |
| ||||
|
|
解答:解:(Ⅰ)在正方形ADEF中,ED⊥AD.
又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD.
所以ED⊥BC.(3分)
在直角梯形ABCD中,AB=AD=1,CD=2,可得BC=
.
在△BCD中,BD=BC=
,CD=2,
所以BD2+BC2=CD2.
所以BC⊥BD.(5分)
所以BC⊥平面BDE.(6分)
(Ⅱ)DE,DA,DC两两垂直,以D为顶点,DA,DC,DE分别为x轴y轴z轴,建立直角坐标系D-xyz,
则D(0,0,0),A(2,0,0),E(0,0,2),B(2,2,0),F(2,0,2)
=(2,0,0),
=(2,2,-2)设P(o,y,z)则|y|=|z|.
令
=(x′,y′,z′)是平面BEF的法向量,则
,
∴
令y′=1,得
∴
=(0,1,1)
∵AP与平面BEF所成的角等于30°
∴
与
所成的角为60°或120°.
∴cos<
,
>=
=
=
.
∴y2+z2+4yz-4=0
又∵|y|=|z|.
∴y=z或y=-z,当y=z时y=z=±
,
当y=-z时,上式无解,
∴P(0,
,
),或P(0,-
,-
).
又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD.
所以ED⊥BC.(3分)
在直角梯形ABCD中,AB=AD=1,CD=2,可得BC=
| 2 |
在△BCD中,BD=BC=
| 2 |
所以BD2+BC2=CD2.
所以BC⊥BD.(5分)
所以BC⊥平面BDE.(6分)
(Ⅱ)DE,DA,DC两两垂直,以D为顶点,DA,DC,DE分别为x轴y轴z轴,建立直角坐标系D-xyz,
则D(0,0,0),A(2,0,0),E(0,0,2),B(2,2,0),F(2,0,2)
| EF |
| EB |
令
| n |
|
∴
|
令y′=1,得
|
∴
| n |
∵AP与平面BEF所成的角等于30°
∴
| AP |
| n |
∴cos<
| AP |
| n |
| ||||
|
|
| |y+z| | ||||
|
| 1 |
| 2 |
∴y2+z2+4yz-4=0
又∵|y|=|z|.
∴y=z或y=-z,当y=z时y=z=±
| ||
| 3 |
当y=-z时,上式无解,
∴P(0,
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
点评:本题考查直线与平面垂直,直线与平面所成的角,空间向量的运算,考查空间想象能力,计算能力已经逻辑推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 使得
使得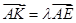 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为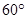 ,求
,求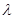 的值。
的值。
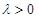 使得
使得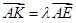 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为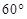 ,求
,求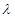 的值。
的值。
 使得
使得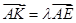 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为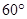 ,求
,求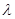 的值。
的值。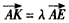 ,KF与平面ABG所成角为30°,求λ的值。
,KF与平面ABG所成角为30°,求λ的值。