题目内容
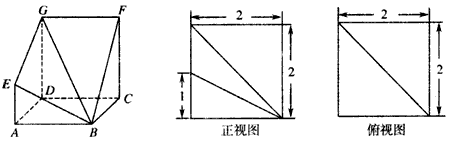
如图,多面体ABCD-EFG中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图、俯视图如下:
(I)求证:平面AEF⊥平面BDG;
(II)若存在λ>0使得
| AK |
| AE |
分析:(I)求证:平面AEF⊥平面BDG,由面面垂直的判定定理,先证线面垂直,再证面面垂直.由图形知,可请AC⊥面BDG
(II)先假设其存在,作出相应瓣辅助线,表示出二面角,由二面角为为60°,建立关于λ的方程求求值.
(II)先假设其存在,作出相应瓣辅助线,表示出二面角,由二面角为为60°,建立关于λ的方程求求值.
解答:解:(I)连AC,BD,在正方形ABCD中,AC⊥BD,
又∵
?
又AC?面ABCD,可得AC⊥GD,又AC⊥BD,GD,则AC⊥面BDG,
又由AE与FC共面,可得出平面AEF即平面AEFC,
又AC?面AEFC,故面AEFC⊥面BDG
(II)作KO⊥AG于0,OH⊥BG于H,连KH,由AE⊥面ABCD,得AE⊥AB,且正方形ABCD中,AD⊥AB,故有AB⊥面ADE,
又AE∥GD,得A,E,G,D共面,且KO?面ADE,可得出AB⊥KO,故可得出KO⊥面ABG,则OH是KH在平面ABG的射影,
又OH⊥BG且BG?平面ABG,可得出KH⊥BG,且OH⊥BG,则∠KHO是二面角A-BG-K的平面角,∠KHO=60°
由正视图知,AE=1,所以AK=λ,
又AD=GD=2,AE∥GD,AE⊥平面ABCD,可得出GD⊥面ABCD,进而推出GD⊥AD,故得∠DATG=∠KAG=45°,且AG=2
,由此可得出KO=
λ,AO=
λ,GO=AG=-AO=2,
作AH'⊥BG于H′,则AH'=
=2
×
=
∴OH=
×AH′=
×2×
=
,tan∠KHO=
=
,
∴
=
,
∴λ=2
又∵
|
|
又AC?面ABCD,可得AC⊥GD,又AC⊥BD,GD,则AC⊥面BDG,
又由AE与FC共面,可得出平面AEF即平面AEFC,
又AC?面AEFC,故面AEFC⊥面BDG
(II)作KO⊥AG于0,OH⊥BG于H,连KH,由AE⊥面ABCD,得AE⊥AB,且正方形ABCD中,AD⊥AB,故有AB⊥面ADE,
又AE∥GD,得A,E,G,D共面,且KO?面ADE,可得出AB⊥KO,故可得出KO⊥面ABG,则OH是KH在平面ABG的射影,
又OH⊥BG且BG?平面ABG,可得出KH⊥BG,且OH⊥BG,则∠KHO是二面角A-BG-K的平面角,∠KHO=60°
由正视图知,AE=1,所以AK=λ,
又AD=GD=2,AE∥GD,AE⊥平面ABCD,可得出GD⊥面ABCD,进而推出GD⊥AD,故得∠DATG=∠KAG=45°,且AG=2
| 2 |
| ||
| 2 |
| ||
| 2 |
作AH'⊥BG于H′,则AH'=
| AB×AG |
| BG |
|
| OH |
| AH |
| OG |
| AG |
∴OH=
| OG |
| AG |
2
| ||||||
2
|
|
| ||||
|
| KO |
| OH |
| 3 |
∴
| ||||||||
|
| 3 |
∴λ=2
点评:本题考查了立体几何中面面垂直的判定定理以及利用二面角的大小建立方程求参数,本题中第二小题难度较大,线面关系、线线关系以及面面关系都有涉及,综合性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

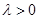 使得
使得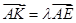 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为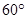 ,求
,求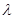 的值。
的值。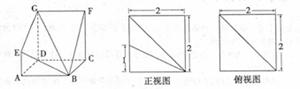
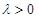 使得
使得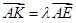 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为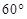 ,求
,求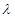 的值。
的值。
 使得
使得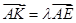 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为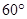 ,求
,求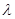 的值。
的值。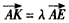 ,KF与平面ABG所成角为30°,求λ的值。
,KF与平面ABG所成角为30°,求λ的值。