题目内容
设Rt△ABC的三边分别为a,b,c,其中c为斜边,m]直线ax+by+c=0与圆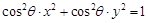 ,(
,(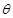 为常数,
为常数,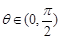 )交于
)交于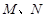 两点,则
两点,则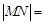
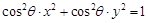 ,(
,(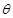 为常数,
为常数,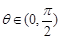 )交于
)交于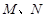 两点,则
两点,则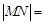
| A.sinθ | B.2sinθ | C.tanθ | D.2tanθ |
D
分析:根据圆的方程求出圆心和半径,根据点到直线的距离公式求出圆心O到直线ax+by+c=0的距离等于d,由弦长公式
|MN|="2"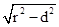 ,运算求得结果.
,运算求得结果.
解答:解:圆cos2θ?x2+cos2θ?y2=1,即 x2+y2=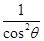 ,表示以原点O为圆心,以|
,表示以原点O为圆心,以|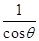 |为半径的圆.
|为半径的圆.
由于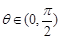 ,故半径为 r=
,故半径为 r=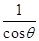 .
.
∵直角△ABC的三边分别为a,b,c,其中c为斜边,∴c2=a2+b2.
圆心O到直线ax+by+c=0的距离等于d=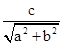 =1,
=1,
故弦长|MN|=2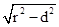 ="2"
="2" 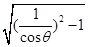 =2tanθ.
=2tanθ.
故选D.
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,属于中档题.
|MN|="2"
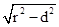 ,运算求得结果.
,运算求得结果.解答:解:圆cos2θ?x2+cos2θ?y2=1,即 x2+y2=
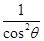 ,表示以原点O为圆心,以|
,表示以原点O为圆心,以|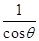 |为半径的圆.
|为半径的圆.由于
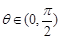 ,故半径为 r=
,故半径为 r=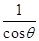 .
.∵直角△ABC的三边分别为a,b,c,其中c为斜边,∴c2=a2+b2.
圆心O到直线ax+by+c=0的距离等于d=
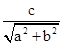 =1,
=1,故弦长|MN|=2
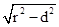 ="2"
="2" 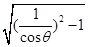 =2tanθ.
=2tanθ.故选D.
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,属于中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
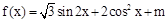 在区间[
在区间[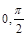 ]上的最大值为6,
]上的最大值为6,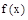 关于y轴的对称图象得函数
关于y轴的对称图象得函数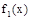 的图象,再把
的图象,再把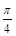 个单位得
个单位得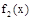 的图象,求函数
的图象,求函数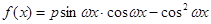
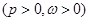 的最大值为
的最大值为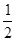 ,小正周期为
,小正周期为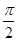 .
.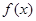 的解析式;
的解析式;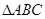 的三条边为
的三条边为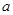 ,
,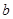 ,
,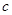 ,满足
,满足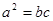 ,
,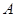 .求角
.求角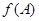 的值域.
的值域.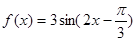 的图象为
的图象为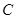 .有以下结论,其中正确的个数为( )
.有以下结论,其中正确的个数为( )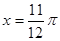 对称; ②函数
对称; ②函数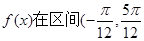 )内是增函数;
)内是增函数;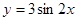 的图象向右平移
的图象向右平移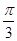 个单位长度可以得到图象
个单位长度可以得到图象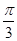 )的图象,只要将y=sin2x的图象 ( )
)的图象,只要将y=sin2x的图象 ( )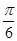 个单位
个单位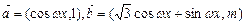 ,函数
,函数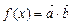 (其中
(其中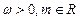 ).且
).且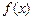 的图像在y轴右侧的第一个最高点的横坐标是
的图像在y轴右侧的第一个最高点的横坐标是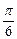
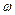 的值和
的值和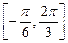 上的最小值为
上的最小值为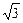 ,求m的值
,求m的值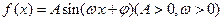 的部分
的部分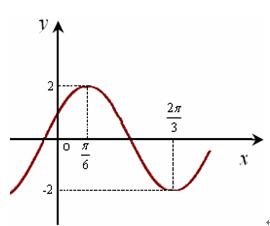
 时,求该函数图象的对称轴方程和对称中心坐标;(4分)
时,求该函数图象的对称轴方程和对称中心坐标;(4分)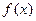 的单调增区间;(3分)
的单调增区间;(3分)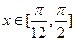 ,求
,求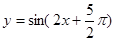 的一个对称中心是 ( )
的一个对称中心是 ( )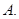
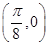
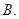
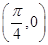
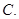
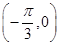

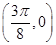
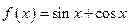 ,给出以
,给出以 下四个命题:
下四个命题: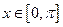 ,则
,则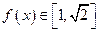
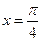 是函数
是函数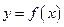 图象的一条对称轴
图象的一条对称轴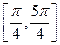 上函数
上函数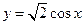 的图象向右平移
的图象向右平移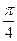 个单位而得到.
个单位而得到.