题目内容
设P(x,y)是曲线 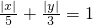 上的点,F1(-4,0),F2(4,0),则
上的点,F1(-4,0),F2(4,0),则
- A.|PF1|+|PF2|<10
- B.|PF1|+|PF2|≤10
- C.|PF1|+|PF2|>10
- D.|PF1|+|PF2|≥10
B
分析:根据曲线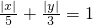 ,可以联想椭圆方程
,可以联想椭圆方程 ,可知方程
,可知方程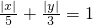 对应的曲线为连接椭圆四个顶点围成的四边形,并且四边形在椭圆的内部(四个顶点在椭圆上).利用椭圆的定义可得结论
对应的曲线为连接椭圆四个顶点围成的四边形,并且四边形在椭圆的内部(四个顶点在椭圆上).利用椭圆的定义可得结论
解答:根据曲线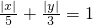 ,可以联想椭圆方程
,可以联想椭圆方程 ,方程
,方程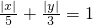 对应的曲线表示四条线段围成的四边形,四个顶点的坐标分别为(5,0),(0,3),(-5,0),(0,-3)
对应的曲线表示四条线段围成的四边形,四个顶点的坐标分别为(5,0),(0,3),(-5,0),(0,-3)
∵椭圆 四个顶点的坐标分别为(5,0),(0,3),(-5,0),(0,-3)
四个顶点的坐标分别为(5,0),(0,3),(-5,0),(0,-3)
∴方程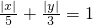 对应的曲线为连接椭圆四个顶点围成的四边形,并且四边形在椭圆的内部(四个顶点在椭圆上).
对应的曲线为连接椭圆四个顶点围成的四边形,并且四边形在椭圆的内部(四个顶点在椭圆上).
根据椭圆的定义,当点P在椭圆上时,|PF1|+|PF2|=10
点P在椭圆内部时,|PF1|+|PF2|<10
∴|PF1|+|PF2|≤10
故选B.
点评:本题以曲线为载体,考查类比思想,考查椭圆的定义,正确的类比联想椭圆方程是解题的关键.
分析:根据曲线
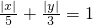 ,可以联想椭圆方程
,可以联想椭圆方程 ,可知方程
,可知方程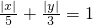 对应的曲线为连接椭圆四个顶点围成的四边形,并且四边形在椭圆的内部(四个顶点在椭圆上).利用椭圆的定义可得结论
对应的曲线为连接椭圆四个顶点围成的四边形,并且四边形在椭圆的内部(四个顶点在椭圆上).利用椭圆的定义可得结论解答:根据曲线
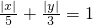 ,可以联想椭圆方程
,可以联想椭圆方程 ,方程
,方程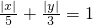 对应的曲线表示四条线段围成的四边形,四个顶点的坐标分别为(5,0),(0,3),(-5,0),(0,-3)
对应的曲线表示四条线段围成的四边形,四个顶点的坐标分别为(5,0),(0,3),(-5,0),(0,-3)∵椭圆
 四个顶点的坐标分别为(5,0),(0,3),(-5,0),(0,-3)
四个顶点的坐标分别为(5,0),(0,3),(-5,0),(0,-3)∴方程
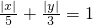 对应的曲线为连接椭圆四个顶点围成的四边形,并且四边形在椭圆的内部(四个顶点在椭圆上).
对应的曲线为连接椭圆四个顶点围成的四边形,并且四边形在椭圆的内部(四个顶点在椭圆上).根据椭圆的定义,当点P在椭圆上时,|PF1|+|PF2|=10
点P在椭圆内部时,|PF1|+|PF2|<10
∴|PF1|+|PF2|≤10
故选B.
点评:本题以曲线为载体,考查类比思想,考查椭圆的定义,正确的类比联想椭圆方程是解题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目