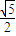题目内容
(中诱导公式、基本公式)若cos(α+π)=
,π≤α<2π,则sin(-α-2π)的值是( )
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
分析:本题考查的知识点是运用诱导公式进行化简求值,及同角三角函数间的关系,由cos(α+π)=
,π≤α<2π,我们易根据诱导公式结合同角三角函数关系求出sinα的值,然而sin(-α-2π)=-sinα.
| 3 |
| 5 |
解答:解:∵cos(α+π)=-cosα=
,
π<α<2π,
∴π<α<
.
则sinα<0
sin(-α-2π)=-sin(α+2π)=-sinα=
=
故选C
| 3 |
| 5 |
π<α<2π,
∴π<α<
| 3π |
| 2 |
则sinα<0
sin(-α-2π)=-sin(α+2π)=-sinα=
| 1-cos2α |
| 4 |
| 5 |
故选C
点评:三角函数给值求值问题中,根据该角的一个三角函数值,求另一个三角函数值,我们要根据角的位置对符号进行判断.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(中诱导公式、基本公式)已知sin(π-α)=-
,且α∈(-
,0),则tan(2π-α)的值为( )
| 2 |
| 3 |
| π |
| 2 |
A、-
| ||||
B、
| ||||
C、±
| ||||
D、
|
 ,则sin(-α-2π)的值是( )
,则sin(-α-2π)的值是( )



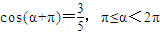 ,则sin(-α-2π)的值是( )
,则sin(-α-2π)的值是( )



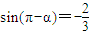 ,且
,且 ,则tan(2π-α)的值为( )
,则tan(2π-α)的值为( )