题目内容
口袋中有质地、大小完全相同的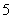 个球,编号分别为
个球,编号分别为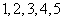 ,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(1)求甲赢且编号的和为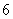 的事件发生的概率;
的事件发生的概率;
(2)这种游戏规则公平吗?试说明理由.
【答案】
【解析】(1)设“甲胜且两数字之和为6”为事件A,事件A包含的基本事件为
(1,5),(2,4),(3,3),(4,2),(5,1),共 个.……………………2分
个.……………………2分
又甲、乙二人取出的数字共有5×5=25(个)等可能的结果,………4分
所以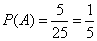 . ……………………………………………………………5分
. ……………………………………………………………5分
答:编号的和为6的概率为 .………………………………………6分
.………………………………………6分
(2)这种游戏规则不公平.………7分设“甲胜”为事件B,“乙胜”为事件C,…8分
则甲胜即两数字之和为偶数所包含的基本事件数为13个:
(1,1), (1,3), (1,5), (2,2), (2,4), (3,1), (3,3), (3,5), (4,2), (4,4), (5,1), (5,3), (5,1)
所以甲胜的概率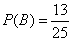 ,从而乙胜的概率
,从而乙胜的概率 .…11分
.…11分
由于P(B)≠P(C),所以这种游戏规则不公平. ………………………………12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目