题目内容
口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.(1)甲、乙按以上规则各摸一个球,求事件“甲赢且编号的和为6”发生的概率;
(2)这种游戏规则公平吗?试说明理由.
分析:(1)由题意知本题是一个等可能事件的概率,试验发生包含的事件是甲、乙二人取出的数字共有5×5等可能的结果,满足条件的事件包含的基本事件可以列举出,根据概率公式得到结果.
(2)这种游戏规则不公平,甲胜即两数字之和为偶数所包含的基本事件数为13个,做出甲胜的概率,根据对立事件的概率做出乙胜的概率,两者相比较得到结论.
(2)这种游戏规则不公平,甲胜即两数字之和为偶数所包含的基本事件数为13个,做出甲胜的概率,根据对立事件的概率做出乙胜的概率,两者相比较得到结论.
解答:解:(1)由题意知本题是一个等可能事件的概率,
设“甲胜且两数字之和为6”为事件A,事件A包含的基本事件为
(1,5),(2,4)(3,3),(4,2),(5,1)共5个.
又甲、乙二人取出的数字共有5×5=25等可能的结果,
∴P(A)=
=
.
即编号的和为6的概率为
.
(2)这种游戏规则不公平.
设甲胜为事件B,乙胜为事件C,
则甲胜即两数字之和为偶数所包含的基本事件数为13个:
(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),
(3,3),(3,5),(4,2),(4,4),(5,1),(5,3),(5,5).
∴甲胜的概率P(B)=
,
从而乙胜的概率P(C)=1-
=
.
由于P(B)≠P(C),
∴这种游戏规则不公平.
设“甲胜且两数字之和为6”为事件A,事件A包含的基本事件为
(1,5),(2,4)(3,3),(4,2),(5,1)共5个.
又甲、乙二人取出的数字共有5×5=25等可能的结果,
∴P(A)=
| 5 |
| 25 |
| 1 |
| 5 |
即编号的和为6的概率为
| 1 |
| 5 |
(2)这种游戏规则不公平.
设甲胜为事件B,乙胜为事件C,
则甲胜即两数字之和为偶数所包含的基本事件数为13个:
(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),
(3,3),(3,5),(4,2),(4,4),(5,1),(5,3),(5,5).
∴甲胜的概率P(B)=
| 13 |
| 25 |
从而乙胜的概率P(C)=1-
| 13 |
| 25 |
| 12 |
| 25 |
由于P(B)≠P(C),
∴这种游戏规则不公平.
点评:本题主要考查古典概型,解决古典概型问题时最有效的工具是列举,大纲中要求能通过列举解决古典概型问题,也有一些题目需要借助于排列组合来计数.

练习册系列答案
相关题目
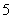 个球,编号分别为
个球,编号分别为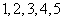 ,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.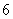 的事件发生的概率;
的事件发生的概率;