题目内容
已知函数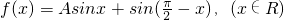 .且
.且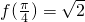 ,
,
(1)求函数f(x)的单调减区间;
(2)求函数f(x)的最大值与取得最大值时x的集合;
(3)若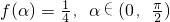 ,求sin2α的值.
,求sin2α的值.
解:(1) =Asinx+cosx
=Asinx+cosx
∵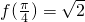 ,∴
,∴ ,∴A=1
,∴A=1
∴f(x)=sinx+cosx= sin(x+
sin(x+ )
)
令x+ ∈
∈ (k∈Z),可得x∈
(k∈Z),可得x∈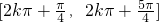 (k∈Z)
(k∈Z)
即函数f(x)的单调减区间为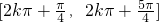 (k∈Z);
(k∈Z);
(2)令x+ =
= ,可得x=
,可得x= (k∈Z),此时求函数f(x)取到最大值
(k∈Z),此时求函数f(x)取到最大值 ;
;
(3)∵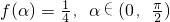 ,
,
∴sinα+cosα=
两边平方可得1+sin2α=
∴sin2α=-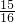 .
.
分析:(1)利用诱导公式及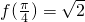 ,求出函数解析式,从而可得函数f(x)的单调减区间;
,求出函数解析式,从而可得函数f(x)的单调减区间;
(2)利用正弦函数的性质,可得函数f(x)的最大值与取得最大值时x的集合;
(3)由条件可得sinα+cosα= ,两边平方可得sin2α的值.
,两边平方可得sin2α的值.
点评:本题考查三角函数的化简,考查三角函数的性质,属于中档题.
 =Asinx+cosx
=Asinx+cosx∵
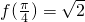 ,∴
,∴ ,∴A=1
,∴A=1∴f(x)=sinx+cosx=
 sin(x+
sin(x+ )
)令x+
 ∈
∈ (k∈Z),可得x∈
(k∈Z),可得x∈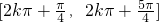 (k∈Z)
(k∈Z)即函数f(x)的单调减区间为
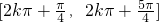 (k∈Z);
(k∈Z);(2)令x+
 =
= ,可得x=
,可得x= (k∈Z),此时求函数f(x)取到最大值
(k∈Z),此时求函数f(x)取到最大值 ;
;(3)∵
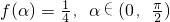 ,
,∴sinα+cosα=

两边平方可得1+sin2α=

∴sin2α=-
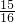 .
.分析:(1)利用诱导公式及
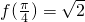 ,求出函数解析式,从而可得函数f(x)的单调减区间;
,求出函数解析式,从而可得函数f(x)的单调减区间;(2)利用正弦函数的性质,可得函数f(x)的最大值与取得最大值时x的集合;
(3)由条件可得sinα+cosα=
 ,两边平方可得sin2α的值.
,两边平方可得sin2α的值.点评:本题考查三角函数的化简,考查三角函数的性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,且f(1)=2,
,且f(1)=2,
 ,且f(1)=1,f(-2)=4.
,且f(1)=1,f(-2)=4. 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. (
( 且
且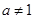 )
)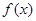 在
在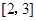 上的最大值与最小值的和为2,求
上的最大值与最小值的和为2,求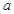 的值;
的值;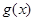 的图象,写函数
的图象,写函数 (
( 且
且 ).
).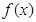 的单调区间;
的单调区间;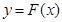 的图象为曲线
的图象为曲线 .设点
.设点 ,
, 是曲线
是曲线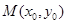 ,使得:①
,使得:① ;②曲线
;②曲线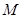 处的切线平行于直线
处的切线平行于直线 ,则称函数
,则称函数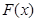 存在“中值相依切线”. 试问:函数
存在“中值相依切线”. 试问:函数 ,且
,且 ,
,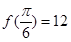
 的最大值及取得最大值时
的最大值及取得最大值时 的值。
的值。