题目内容
(本题满分12分)已知一动圆与圆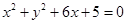 外切,同时与圆
外切,同时与圆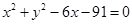 内切.
内切.
(1)求动圆圆心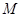 的轨迹方程,并说明它是什么样的曲线;
的轨迹方程,并说明它是什么样的曲线;
(2)直线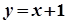 与M的轨迹相交于不同的两点
与M的轨迹相交于不同的两点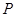 、
、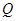 ,求
,求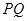 的中点的坐标;
的中点的坐标;
(3)求(2)中△OPQ的面积(O为坐标原点).
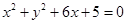 外切,同时与圆
外切,同时与圆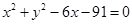 内切.
内切.(1)求动圆圆心
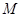 的轨迹方程,并说明它是什么样的曲线;
的轨迹方程,并说明它是什么样的曲线;(2)直线
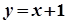 与M的轨迹相交于不同的两点
与M的轨迹相交于不同的两点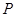 、
、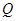 ,求
,求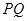 的中点的坐标;
的中点的坐标;(3)求(2)中△OPQ的面积(O为坐标原点).
(1)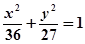 (2)
(2)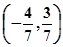 (3 )
(3 ) 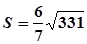
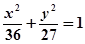 (2)
(2)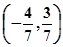 (3 )
(3 ) 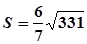
圆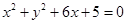 的圆心为A(-3,0),半径为2;圆
的圆心为A(-3,0),半径为2;圆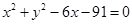 的圆心为B(3,0),半径为10;设动圆圆心为
的圆心为B(3,0),半径为10;设动圆圆心为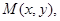 半径为r;则
半径为r;则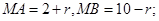
于是 所以动圆圆心
所以动圆圆心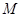 的轨迹是以A(-3,0),B(3,0)为焦点,长轴长为12的椭圆。
的轨迹是以A(-3,0),B(3,0)为焦点,长轴长为12的椭圆。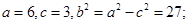
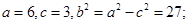 所以M轨迹方程为
所以M轨迹方程为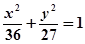
(2)由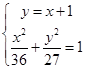 消去y得:
消去y得: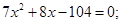 设
设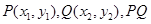 中点为
中点为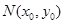 ;则
;则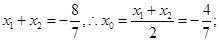
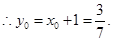 所以PQ中点坐标为
所以PQ中点坐标为
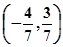 。
。
(3)由(2)知: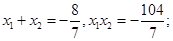 所以
所以
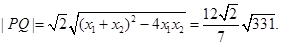 原点到直线
原点到直线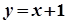 的距离为
的距离为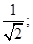 所以
所以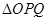 的面积为
的面积为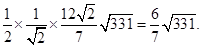
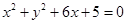 的圆心为A(-3,0),半径为2;圆
的圆心为A(-3,0),半径为2;圆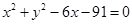 的圆心为B(3,0),半径为10;设动圆圆心为
的圆心为B(3,0),半径为10;设动圆圆心为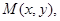 半径为r;则
半径为r;则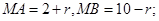
于是
 所以动圆圆心
所以动圆圆心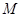 的轨迹是以A(-3,0),B(3,0)为焦点,长轴长为12的椭圆。
的轨迹是以A(-3,0),B(3,0)为焦点,长轴长为12的椭圆。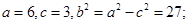
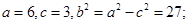 所以M轨迹方程为
所以M轨迹方程为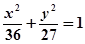
(2)由
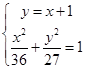 消去y得:
消去y得: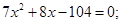 设
设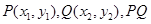 中点为
中点为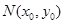 ;则
;则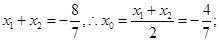
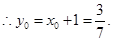 所以PQ中点坐标为
所以PQ中点坐标为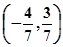 。
。(3)由(2)知:
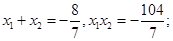 所以
所以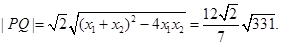 原点到直线
原点到直线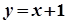 的距离为
的距离为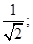 所以
所以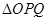 的面积为
的面积为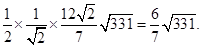

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
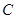 的方程为
的方程为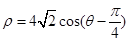 ,以极点为坐标原点
,以极点为坐标原点 ,极轴为
,极轴为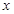 轴的正
轴的正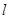 的参数方程为
的参数方程为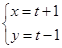 (
(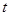 为参数),求直线
为参数),求直线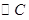 截
截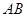 的长度.
的长度.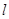 的参数方程为
的参数方程为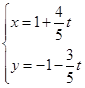 (
(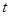 为参数),若以
为参数),若以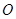 为极点,
为极点,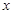 轴正半轴为极轴建立极坐标系,则曲线
轴正半轴为极轴建立极坐标系,则曲线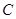 的极坐标方程为
的极坐标方程为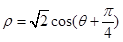 ,则直线
,则直线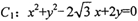 和曲线
和曲线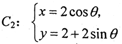 (
(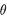 为参数)关于直线l1.对称,直线l2过点
为参数)关于直线l1.对称,直线l2过点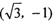 旦与l1的夹角为60° ,则直线l2的方程为
旦与l1的夹角为60° ,则直线l2的方程为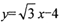

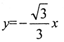
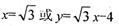
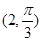 且平行于极轴的直线的极坐标方程为 ※ .
且平行于极轴的直线的极坐标方程为 ※ .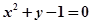 的参数方程为( )
的参数方程为( )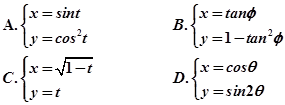
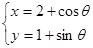 ,
,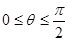 ,则动点p所表示的曲线长度为
,则动点p所表示的曲线长度为  中,曲线
中,曲线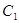 的参数方程为
的参数方程为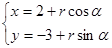 (
(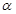 为参数),在极坐标系中(在直角坐标系中,以O为极点,以
为参数),在极坐标系中(在直角坐标系中,以O为极点,以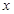 轴正半轴为极轴),曲线
轴正半轴为极轴),曲线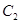 的方程为
的方程为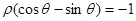 ,若
,若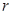 = .
= . 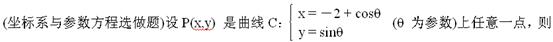
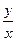 的取值范围是 .
的取值范围是 .