题目内容
设f(x)是定义在R上恒不为零的函数，对任意实数x，y∈R，都有f(x)·f(y)＝f(x＋y)，若a1＝
，an＝f(n)(n∈N*)，则数列{an}前n项和Sn的取值范围是
[ ]
A．[，2)
B．[，2]
C．[，1)
D．[，1]
答案：C
解析：
解析：
|
因f(n＋1)＝f(1)·f(n)，则an+1＝a1·an＝ ∴数列{an}是以 ∴an＝( Sn＝ ∵n∈N*，∴ |
an，
为首项，公比为
＝1－(
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
相关题目
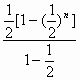]都有f (x1＋x2) = f (x1) ? f (x2)．且f (1) = a＞0．
)；
)，求
．
f(0n)(1-x)n+
f(
)x(1-x)n-1+…+
f(
)xn(1-x)0(x≠0,1).
,又当-3≤x≤-2时，f(x)=2x,则f(113.5)的值是（ ）
B.-
C.
D.-
)x－1，若在区间(－2，6]内关于x的方程f(x)－loga(x＋2)＝0(a＞1)恰有3个不同的实数根，则a的取值范围是
) D. (