题目内容
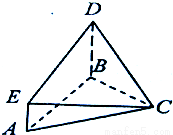
已知BD⊥平面ABC,AE∥BD,△ABC是正三角形,AB=BD=2AE=2.
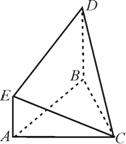 (1)求证:平面CDE⊥平面BCD;
(1)求证:平面CDE⊥平面BCD;
(2)求点A到平面CDE的距离;
(3)求平面CDE与平面ABC所成角的大小.
(Ⅰ) 略 (Ⅱ) ![]() (Ⅲ)45°
(Ⅲ)45°
解析:
(1)证明:取CD、BC的中点F、G,连EF、FG、AG …
(1分)
∵FG![]()
![]() BD,AE
BD,AE![]()
![]() BD ∴AE
BD ∴AE![]() FG ∴AG
FG ∴AG![]() EF ………(2分)
EF ………(2分)
∵△ABC为正三角形,G是BC的中点∴AG⊥BC∵BD⊥平面ABC,AG![]() 平面ABC
平面ABC
∴BD⊥AG∴AG⊥平面BCD ………(3分)
∴EF⊥平面BCD∵EF![]() 平面CDE∴平面CDE⊥平面BCD(4分)
平面CDE∴平面CDE⊥平面BCD(4分)
(2)由(1)知AG∥平面CDE,则点G到平面CDE的距离为所求. ……(5分)
过G作GH⊥CD于H,由于平面CDE⊥平面BCD,所以GH⊥平面CDE………(6分)
∵BD=BC=2,∠CBD=90°,∴∠BCD=45°∵GC=![]() BC=1 ∴GH=
BC=1 ∴GH=![]()
即点A到平面CDE的距离为![]() ……(8分)
……(8分)
(3)延长BA与DE交于M点,连CM,过A作AN⊥CM于N,连EN,
则∠ENA为所求二面角的平面角. …………(10分)
可知AM=AC=2,∠CAM=120°
∴AN=1 ∵AE=1 ∴![]() ∴
∴![]()
即所求的二面角的大小为45° …………(12分)

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
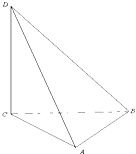 如图,直三棱锥D-ABC,已知DC⊥平面ABC,AB=20米,从点A处看到点D的仰角为60°,∠ABC=30°,∠BAC=105°,分别求AD、BD的长(精确到0.01米)
如图,直三棱锥D-ABC,已知DC⊥平面ABC,AB=20米,从点A处看到点D的仰角为60°,∠ABC=30°,∠BAC=105°,分别求AD、BD的长(精确到0.01米) 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥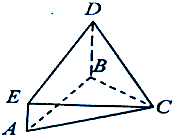 (2011•黄冈模拟)如图,已知BD⊥平面ABC,AE∥BD,△ABC是等腰直角三角形,∠C=90°AB=BD=2AE,则面CDE与面ABC所成的角的正切值为
(2011•黄冈模拟)如图,已知BD⊥平面ABC,AE∥BD,△ABC是等腰直角三角形,∠C=90°AB=BD=2AE,则面CDE与面ABC所成的角的正切值为