题目内容
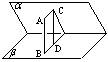
如图,已知BD⊥平面ABC,AE∥BD,△ABC是等腰直角三角形,∠C=90°AB=BD=2AE,则面CDE与面ABC所成的角的正切值为 .
【答案】分析:由于是无棱二面角,故先作出二面角的棱,再利用定义作出平面角,从而利用直角三角形求二面角的平面角.
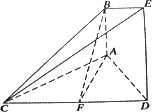
解答:解:延长BA到G,使AG=AB,连GE,GC
不妨设AE=1,则AB=BD=2,CA=CB=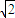 ,取AB中点F,连CF,则CF⊥AB,且FA=FB=FC=1,故CG=
,取AB中点F,连CF,则CF⊥AB,且FA=FB=FC=1,故CG=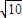
设∠CGF=α,则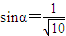 ,作BH⊥GC延长线于H,令∠BHD=θ
,作BH⊥GC延长线于H,令∠BHD=θ
则θ为面CDE与面ABC所成的角
∵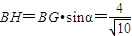
∴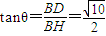
∴面CDE与面ABC所成的角的正切值为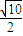
故答案为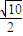
点评:本题的考点是二面角的平面角及求法,主要考查求解二面角的平面角,关键是找出二面角的棱,作出二面角的平面角,再进行求解.
解答:解:延长BA到G,使AG=AB,连GE,GC
不妨设AE=1,则AB=BD=2,CA=CB=
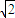 ,取AB中点F,连CF,则CF⊥AB,且FA=FB=FC=1,故CG=
,取AB中点F,连CF,则CF⊥AB,且FA=FB=FC=1,故CG=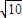
设∠CGF=α,则
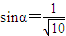 ,作BH⊥GC延长线于H,令∠BHD=θ
,作BH⊥GC延长线于H,令∠BHD=θ则θ为面CDE与面ABC所成的角
∵
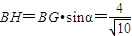
∴
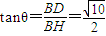
∴面CDE与面ABC所成的角的正切值为
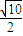
故答案为
点评:本题的考点是二面角的平面角及求法,主要考查求解二面角的平面角,关键是找出二面角的棱,作出二面角的平面角,再进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
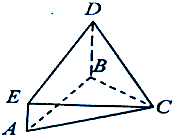 (2011•黄冈模拟)如图,已知BD⊥平面ABC,AE∥BD,△ABC是等腰直角三角形,∠C=90°AB=BD=2AE,则面CDE与面ABC所成的角的正切值为
(2011•黄冈模拟)如图,已知BD⊥平面ABC,AE∥BD,△ABC是等腰直角三角形,∠C=90°AB=BD=2AE,则面CDE与面ABC所成的角的正切值为