题目内容
设偶函数 (
( 为常数)且
为常数)且 的最小值为-6.
的最小值为-6.
(Ⅰ)求 的值;
的值;
(Ⅱ)设 ,
, ,
, ,且
,且 的图像关于直线
的图像关于直线 对称和点
对称和点 对称,若
对称,若 在
在 上单调递增,求
上单调递增,求 和
和 的值.
的值.
 (
( 为常数)且
为常数)且 的最小值为-6.
的最小值为-6.(Ⅰ)求
 的值;
的值; (Ⅱ)设
 ,
, ,
, ,且
,且 的图像关于直线
的图像关于直线 对称和点
对称和点 对称,若
对称,若 在
在 上单调递增,求
上单调递增,求 和
和 的值.
的值.解:(Ⅰ)化简得: ………………………1分
………………………1分
 为偶函数,
为偶函数, ,得
,得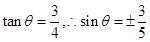 ,…………………2分
,…………………2分

 ……………………5分
……………………5分
(Ⅱ)化简得:
依题有:


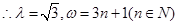
 …………………7分
…………………7分

 在
在 上单调递增
上单调递增 ,
,
 ,经检验
,经检验 (舍)………………………9分
(舍)………………………9分
综上, ………………………10分
………………………10分
 ………………………1分
………………………1分 为偶函数,
为偶函数, ,得
,得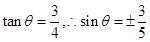 ,…………………2分
,…………………2分
 ……………………5分
……………………5分(Ⅱ)化简得:

依题有:



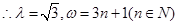
 …………………7分
…………………7分
 在
在 上单调递增
上单调递增 ,
,
 ,经检验
,经检验 (舍)………………………9分
(舍)………………………9分综上,
 ………………………10分
………………………10分本试题主要是考查了三角函数的图像与性质的综合运用。
(1)根据已知条件得到化简得: ………………………1分
………………………1分
 为偶函数,
为偶函数, ,得
,得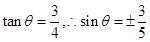 ,从而化简得到求解。
,从而化简得到求解。
(2)化简得:
依题有:
因为设 ,
, ,
, ,且
,且 的图像关于直线
的图像关于直线 对称和点
对称和点 对称,若
对称,若 在
在 上单调递增,可知得到其范围。
上单调递增,可知得到其范围。
(1)根据已知条件得到化简得:
 ………………………1分
………………………1分 为偶函数,
为偶函数, ,得
,得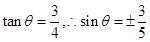 ,从而化简得到求解。
,从而化简得到求解。(2)化简得:

依题有:

因为设
 ,
, ,
, ,且
,且 的图像关于直线
的图像关于直线 对称和点
对称和点 对称,若
对称,若 在
在 上单调递增,可知得到其范围。
上单调递增,可知得到其范围。
练习册系列答案
相关题目
 .
. 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到? ,则下列结论错误的个数是( )
,则下列结论错误的个数是( ) 的值域为
的值域为 ②
② 对称
对称 上递增 ④
上递增 ④

 一个周期的图象如图所示. (1)求函数
一个周期的图象如图所示. (1)求函数 的表达式;(2)若
的表达式;(2)若 ,且A为△ABC的一个内角,求:
,且A为△ABC的一个内角,求: 的值.
的值.
 的图象,只要把函数
的图象,只要把函数 的图象上所有点的
的图象上所有点的 倍(纵坐标不变),再把所得图象上所有的点向左平移
倍(纵坐标不变),再把所得图象上所有的点向左平移 个单位长度。
个单位长度。 个单位长度,再把所得图象上所有的点横坐标缩短到原来的
个单位长度,再把所得图象上所有的点横坐标缩短到原来的

 单调增区间为( )
单调增区间为( )



 的最大值与最小值之和为( )
的最大值与最小值之和为( )

