题目内容
已知点集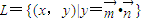
，其中
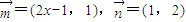，点列Pn（an，bn）在L中，P1为L与y轴的公共点，等差数列{an}的公差为1．（I）求数列{an}，{bn}的通项公式；
（Ⅱ）若
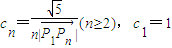，数列{cn}的前n项和Sn满足M+n2Sn≥6n对任意的n∈N*都成立，试求M的取值范围．
【答案】分析：（I）首先运用向量数量积的运算得 
，然后再根据等差通项公式得an=a1+（n-1）×1=n-1，最后再根据bn=2an+1，得bn=2n-1
（Ⅱ）利用条件可得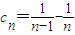
，从而
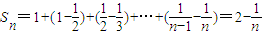，故有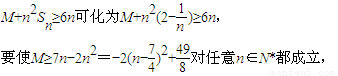
，从而可解．
解答：解：（I）由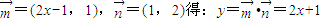
∴L：y=2x+1，P1（0，1），即a1=0，b1=1，故an=n-1，bn=2n-1（n∈N*）
（Ⅱ）当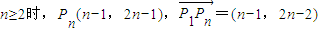
，∴
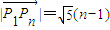
故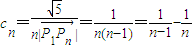
则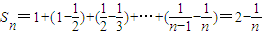
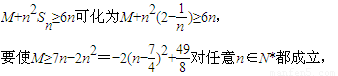
只须M≥6，当且仅当n=2时等号成立，即M的取值范围为M≥6
点评：本题主要考查了数列与向量的综合，考查裂项法求和，同时考查了最值法解决恒成立问题，属于中档题．
，然后再根据等差通项公式得an=a1+（n-1）×1=n-1，最后再根据bn=2an+1，得bn=2n-1（Ⅱ）利用条件可得
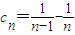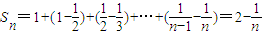，从而，故有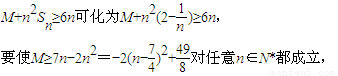，从而可解．解答：解：（I）由
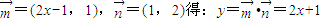
∴L：y=2x+1，P1（0，1），即a1=0，b1=1，故an=n-1，bn=2n-1（n∈N*）
（Ⅱ）当
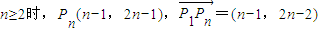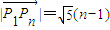
，∴故
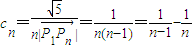
则
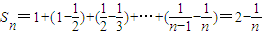
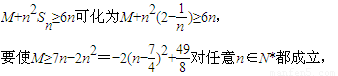
只须M≥6，当且仅当n=2时等号成立，即M的取值范围为M≥6
点评：本题主要考查了数列与向量的综合，考查裂项法求和，同时考查了最值法解决恒成立问题，属于中档题．
练习册系列答案
相关题目
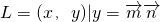，其中
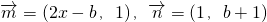，点列Pn（an，bn）在L中，P1为L与y轴的交点，等差数列{an}的公差为1，（n∈N+）
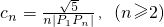，求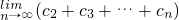
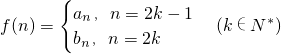，是否存在k∈N+，使得f（k+11）=2f（k），若存在，求出k的值；若不存在，请说明理由．
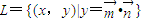，其中
，点列
（
）在L中，
为L与y轴的交点，数列
是公差为1的等差数列．
的通项公式；
令
，试写出
关于
的表达式；
)．是否存在
，使得
，若存在，求出k的值；若不存在，请说明理由.
，其中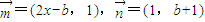
，点列Pn（an，bn）在L中，P1为L与y轴的交点，等差数列{an}的公差为1，n∈N+．
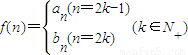，是否存在k∈N+使得f（k+11）=2f（k），若存在，求出k的值；若不存在，请说明理由．
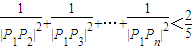（n≥2，n∈N*）．
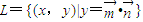，其中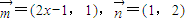
，点列Pn（an，bn）在L中，P1为L与y轴的公共点，等差数列{an}的公差为1．
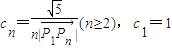，数列{cn}的前n项和Sn满足M+n2Sn≥6n对任意的n∈N*都成立，试求M的取值范围．