题目内容
如图,在矩形ABCD中, ,
,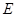 为
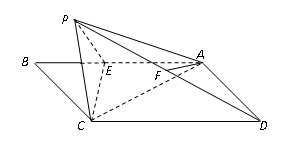
为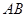 上一点,以直线EC为折线将点B折起至点P,并保持∠PEB为锐角,连结PA、PC、PD,取PD的中点F,若有AF∥平面PEC。
上一点,以直线EC为折线将点B折起至点P,并保持∠PEB为锐角,连结PA、PC、PD,取PD的中点F,若有AF∥平面PEC。
(Ⅰ)试确定点E的位置;
(Ⅱ)若异面直线PE、CD所成的角为60°,求证:平面PEC⊥平面AECD。
【答案】
(Ⅰ)点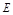 为
为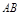 的中点
的中点
(Ⅱ)见解析
【解析】(Ⅰ)点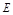 为
为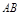 的中点 …………………………………………2分
的中点 …………………………………………2分
证明如下:
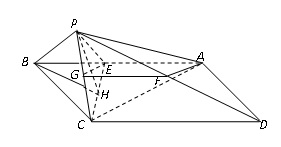
取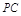 的中点
的中点 ,连
,连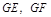 。
。
由条件知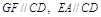 ,
,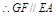 。
。
则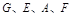 四点共面。
四点共面。
 平面
平面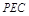 , 平面
, 平面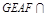 平面
平面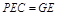 ,
, 。
。
则四边形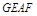 为平行四边形。
为平行四边形。
 .则
.则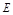 为
为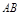 的中点。
的中点。
(Ⅱ)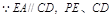 所成的角为
所成的角为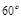 ,∠PEB为锐角,∴∠PEB=60°。
,∠PEB为锐角,∴∠PEB=60°。
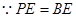 ,∴△PEB为等边三角形。
,∴△PEB为等边三角形。
∴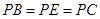 。
。
作PH⊥平面 ,垂足为H,则HB = HE = HC。
,垂足为H,则HB = HE = HC。
∴H为△CBE的外心。
∵△CBE是直角三角形且∠B为直角, ∴外心H为斜边CE的中点。
∴H在CE上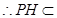 平面
平面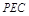 ,∴平面
,∴平面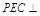 平面
平面 。
。

练习册系列答案
相关题目
 如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD.
如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD. 如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点.
如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点. 如图,在矩形ABCD中,AB=3
如图,在矩形ABCD中,AB=3 如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系: 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=