题目内容
已知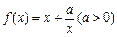 ,当
,当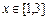 时,
时,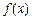 的值域为
的值域为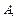 且
且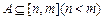 .
.
(1)若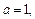 求
求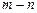 的最小值;
的最小值;
(2)若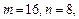 求
求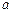 的值;
的值;
(3)若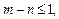 且
且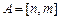 ,求
,求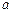 的取值范围.
的取值范围.
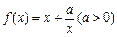 ,当
,当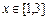 时,
时,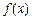 的值域为
的值域为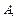 且
且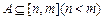 .
.(1)若
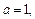 求
求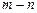 的最小值;
的最小值;(2)若
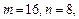 求
求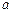 的值;
的值;(3)若
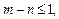 且
且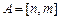 ,求
,求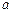 的取值范围.
的取值范围.(Ⅰ)∵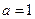 ,∴
,∴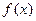 在区间
在区间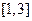 上单调递增,∴
上单调递增,∴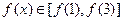 , ┄┄3分
, ┄┄3分
∴当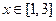 时,
时,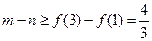 即
即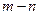 的最小值是
的最小值是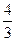 ; ┄┄5分
; ┄┄5分
(Ⅱ)解法一
∵当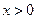 时,
时,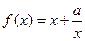 在
在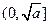 上单调递减,在
上单调递减,在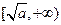 上单调递增,
上单调递增,
∴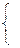
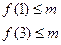
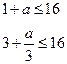
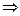
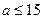 ┄┄┄6分
┄┄┄6分
①当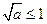 ,即
,即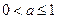 时,
时,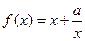 在
在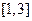 单调递增,
单调递增,
∴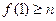 ,
,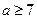 (舍去);
(舍去);
②当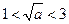 ,即
,即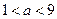 时,
时,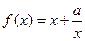 的最小值是
的最小值是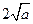 ,
,
∴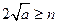 ,
,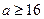 (舍去);
(舍去);
③当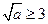 ,即
,即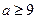 时,
时, 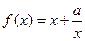 在
在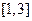 单调递减,
单调递减,
∴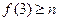 ,
,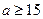 . ┄┄┄9分
. ┄┄┄9分
综上可得: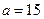 . ┄┄┄10分
. ┄┄┄10分
解法二
当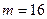 时,
时,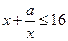 恒成立,即
恒成立,即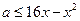 恒成立,
恒成立,
∴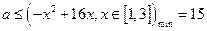 ; ┄┄┄7分
; ┄┄┄7分
当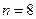 时,
时,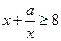 恒成立,即
恒成立,即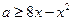 恒成立,
恒成立,
∴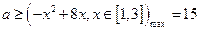 ; ┄┄┄9分
; ┄┄┄9分
综上可得: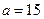 . ┄┄┄10分
. ┄┄┄10分
(Ⅲ)①若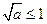 ,即
,即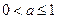 时,
时,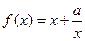 在
在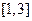 单调递增,
单调递增,
∴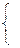
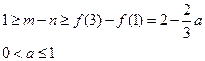 ,无解; ┄┄┄11分
,无解; ┄┄┄11分
②当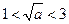 即
即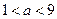 时
时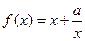 在
在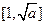 递减,在
递减,在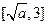 递增,
递增,
∴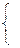
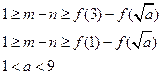
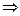
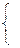
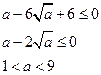
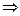
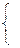
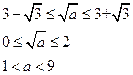
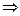
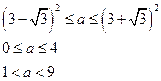
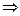
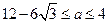 ┄┄┄13分
┄┄┄13分
③当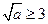 ,即
,即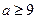 时,函数
时,函数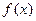 在区间
在区间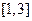 上单调递减,
上单调递减,
∴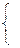
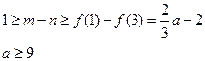 ,无解; ┄┄┄14分
,无解; ┄┄┄14分
综上可得: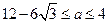 ┄┄┄16分
┄┄┄16分
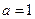 ,∴
,∴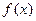 在区间
在区间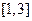 上单调递增,∴
上单调递增,∴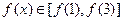 , ┄┄3分
, ┄┄3分∴当
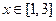 时,
时,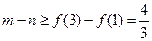 即
即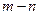 的最小值是
的最小值是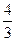 ; ┄┄5分
; ┄┄5分(Ⅱ)解法一
∵当
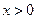 时,
时,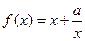 在
在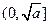 上单调递减,在
上单调递减,在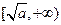 上单调递增,
上单调递增,∴
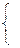
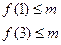
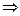
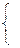
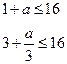
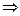
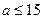 ┄┄┄6分
┄┄┄6分①当
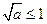 ,即
,即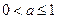 时,
时,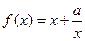 在
在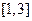 单调递增,
单调递增,∴
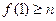 ,
,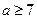 (舍去);
(舍去);②当
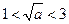 ,即
,即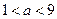 时,
时,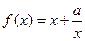 的最小值是
的最小值是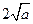 ,
,∴
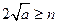 ,
,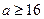 (舍去);
(舍去);③当
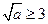 ,即
,即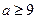 时,
时, 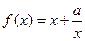 在
在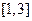 单调递减,
单调递减,∴
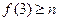 ,
,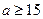 . ┄┄┄9分
. ┄┄┄9分综上可得:
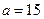 . ┄┄┄10分
. ┄┄┄10分解法二
当
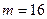 时,
时,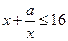 恒成立,即
恒成立,即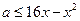 恒成立,
恒成立,∴
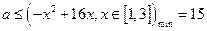 ; ┄┄┄7分
; ┄┄┄7分当
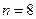 时,
时,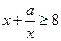 恒成立,即
恒成立,即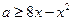 恒成立,
恒成立,∴
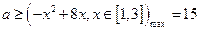 ; ┄┄┄9分
; ┄┄┄9分综上可得:
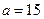 . ┄┄┄10分
. ┄┄┄10分(Ⅲ)①若
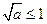 ,即
,即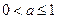 时,
时,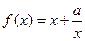 在
在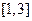 单调递增,
单调递增,∴
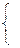
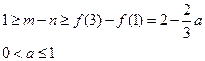 ,无解; ┄┄┄11分
,无解; ┄┄┄11分②当
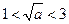 即
即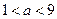 时
时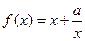 在
在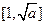 递减,在
递减,在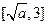 递增,
递增,∴
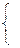
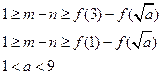
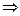
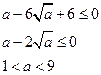
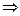
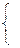
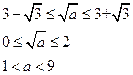
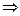
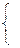
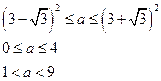
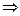
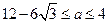 ┄┄┄13分
┄┄┄13分③当
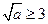 ,即
,即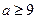 时,函数
时,函数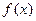 在区间
在区间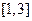 上单调递减,
上单调递减,∴
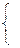
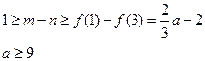 ,无解; ┄┄┄14分
,无解; ┄┄┄14分综上可得:
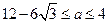 ┄┄┄16分
┄┄┄16分略

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
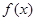 是定义在
是定义在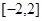 上增函数,且
上增函数,且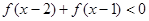 ,求x的取值范围.
,求x的取值范围.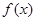 中,在
中,在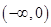 上为递增函数的是 ( )
上为递增函数的是 ( )

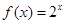
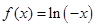
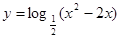 的单调递减区间是__▲_
的单调递减区间是__▲_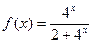 ,
,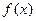 是R上的增函数;(6分)
是R上的增函数;(6分)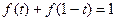 ;(4分)
;(4分)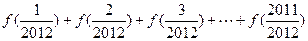 。(4分)
。(4分)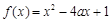 在区间 [-2,4] 上是单调函数的条件是
在区间 [-2,4] 上是单调函数的条件是 


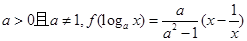 .
.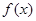 ;(2)判断
;(2)判断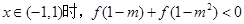 ,求m的集合M。
,求m的集合M。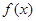 的定义在
的定义在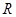 上的偶函数,且是以
上的偶函数,且是以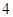 为周期的周期函数,当
为周期的周期函数,当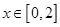 时,
时,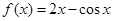 ,则
,则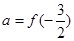 与
与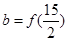 的大小关系为 .
的大小关系为 .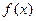 是定义在R上的奇函数,当
是定义在R上的奇函数,当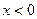 时,
时,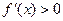 ,且
,且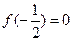 ,则
,则 不等式
不等式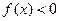 的解集为 .
的解集为 .