题目内容
在一个盒子中有n+2(n≥2,n∈N*)个球,其中2个球的标号是不同的偶数,其余n个球的标号是不同的奇数.甲乙两人同时从盒子中各取出2个球,若这4个球的标号之和为奇数,则甲胜;若这4个球的标号之和为偶数,则乙胜.规定:胜者得2分,负者得0分.(I)当n=3时,求甲的得分ξ的分布列和期望;
(II)当乙胜概率为
| 3 | 7 |
分析:(I)由题意知甲的得分ξ,ξ的可能取值是2,0,当n=3时利用等可能事件的概率做出甲胜的概率,从而得到甲负的概率,写出分布列,做出期望值.
(II)要求乙胜得概率是
时,对应的n的值,对于n的值进行检验,分别做出对应的概率,概率不等于
,则舍去;等于时,的得到结果.
(II)要求乙胜得概率是
| 3 |
| 7 |
| 3 |
| 7 |
解答:解:(I)甲的得分ξ,ξ的可能取值是2,0
当n=3时,甲胜的概率为P=
=
,从而甲负的概率为
.
∴甲的得分ξ的分布列为
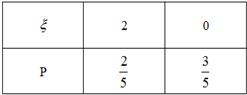
故Eξ=
(II)当n=2时,乙胜的概率为P=1,不合题意;
当n=3时,乙胜的概率为P=
,不合题意;
当n≥4时,乙胜的概率P=
+
=
故
=
,化简得n2-11n+30=0,
解得n=5或n=6.
当n=3时,甲胜的概率为P=
| ||||
|
| 2 |
| 5 |
| 3 |
| 5 |
∴甲的得分ξ的分布列为

故Eξ=
| 4 |
| 5 |
(II)当n=2时,乙胜的概率为P=1,不合题意;
当n=3时,乙胜的概率为P=
| 3 |
| 5 |
当n≥4时,乙胜的概率P=
| ||
|
| ||
|
| (n-2)(n-3)+12 |
| (n+2)(n+1) |
故
| (n-2)(n-3)+12 |
| (n+2)(n+1) |
| 3 |
| 7 |
解得n=5或n=6.
点评:本题考查离散型随机变量的分布列和期望,考查等可能事件的概率,考查分类讨论思想的应用,考查利用概率知识解决实际问题,是一个综合题目.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 时,求n的值.
时,求n的值. 时,求n的值.
时,求n的值. 时,求n的值.
时,求n的值.