题目内容
在一个盒子中有n+2(n≥2,n∈N*)个球,其中2个球的标号是不同的偶数,其余n个球的标号是不同的奇数.甲乙两人同时从盒子中各取出2个球,若这4个球的标号之和为奇数,则甲胜;若这4个球的标号之和为偶数,则乙胜.规定:胜者得2分,负者得0分.
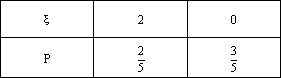
(Ⅰ)当n=3时,求甲的得分ξ的分布列和期望;
(Ⅱ)当乙胜概率为![]() 时,求n的值.
时,求n的值.
答案:
解析:
解析:
|
解:(Ⅰ)当 故甲的得分
6分 故 (Ⅱ)当 当n=3时,乙胜的概率为 当 11分 故 解得 |

练习册系列答案
相关题目
 时,求n的值.
时,求n的值. 时,求n的值.
时,求n的值. 时,求n的值.
时,求n的值.