题目内容
【题目】已知函数f(x)= 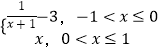 ,若函数g(x)=f(x)﹣mx﹣m在(﹣1,1]内有且仅有两个不同的零点,则实数m的取值范围为 .
,若函数g(x)=f(x)﹣mx﹣m在(﹣1,1]内有且仅有两个不同的零点,则实数m的取值范围为 .
【答案】( ![]() ,﹣2]∪(0,
,﹣2]∪(0,![]() ]
]
【解析】解:由g(x)=f(x)﹣mx﹣m=0,即f(x)=m(x+1),
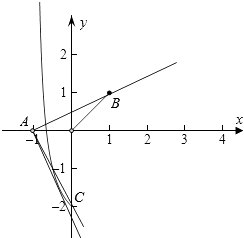
分别作出函数f(x)和y=h(x)=m(x+1)的图象如图:
由图象可知f(1)=1,h(x)表示过定点A(﹣1,0)的直线,
当h(x)过(1,1)时,m= ![]() ,此时两个函数有两个交点,
,此时两个函数有两个交点,
此时满足条件的m的取值范围是0<m≤ ![]() ,
,
当h(x)过(0,﹣2)时,h(0)=﹣2,解得m=﹣2,此时两个函数有两个交点,
当h(x)与f(x)相切时,两个函数只有一个交点,此时 ![]() x﹣3=m(x+1)即m(x+1)2+3(x+1)﹣1=0,
x﹣3=m(x+1)即m(x+1)2+3(x+1)﹣1=0,
当m=0时,只有1解,当m≠0,由△=9+4m=0得m=﹣ ![]() ,此时直线和f(x)相切,
,此时直线和f(x)相切,
∴要使函数有两个零点,则﹣ ![]() <m≤﹣2或0<m≤
<m≤﹣2或0<m≤ ![]() .
.
所以答案是:( ![]() ,﹣2]∪(0,
,﹣2]∪(0, ![]() ].
].

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
【题目】炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,因此必须掌握钢水含碳量和冶炼时间的关系.如果已测得炉料熔化完毕时,钢水的含碳量x与冶炼时间y(从炉料熔化完毕到出钢的时间)的一些数据,如下表所示:
x/0.01% | 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
y/min | 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
(1)作出散点图,你能从散点图中发现含碳量与冶炼时间的一般规律吗?
(2)求回归直线方程.
(3)预测当钢水含碳量为160时,应冶炼多少分钟?