题目内容
数列 ,设其前n项和为Sn,则使Sn<-5成立的自然数n( )
,设其前n项和为Sn,则使Sn<-5成立的自然数n( )A.有最小值63
B.有最大值63
C.有最小值31
D.有最大值31
【答案】分析:根据题中已知数列{an}的通项公式求出其前n项和的Sn的表达式,然后令Sn<-5即可求出n的取值范围,即可知n有最小值.
解答:解:由题意可知;an=log2 (n∈N*),
(n∈N*),
设{an}的前n项和为Sn=log2 +log2
+log2 +…+log2
+…+log2 +log2
+log2 ,
,
=[log22-log23]+[log23-log24]+…+[log2n-log2(n+1)]+[log2(n+1)-log2(n+2)]
=[log22-log2(n+2)]=log2 <-5,
<-5,
即 <2-5
<2-5
解得n+2>64,
n>62;
∴使Sn<-5成立的自然数n有最小值为63.
故选:A.
点评:本题主要考查了数列与函数的综合应用,考查了学生的计算能力和对数列的综合掌握,解题时注意整体思想和转化思想的运用,属于中档题.
解答:解:由题意可知;an=log2
 (n∈N*),
(n∈N*),设{an}的前n项和为Sn=log2
 +log2
+log2 +…+log2
+…+log2 +log2
+log2 ,
,=[log22-log23]+[log23-log24]+…+[log2n-log2(n+1)]+[log2(n+1)-log2(n+2)]
=[log22-log2(n+2)]=log2
 <-5,
<-5,即
 <2-5
<2-5解得n+2>64,
n>62;
∴使Sn<-5成立的自然数n有最小值为63.
故选:A.
点评:本题主要考查了数列与函数的综合应用,考查了学生的计算能力和对数列的综合掌握,解题时注意整体思想和转化思想的运用,属于中档题.

练习册系列答案
相关题目
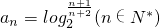 ,设其前n项和为Sn,则使Sn<-5成立的自然数n
,设其前n项和为Sn,则使Sn<-5成立的自然数n