题目内容
设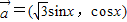 ,
,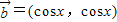 ,记
,记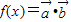 .
.(1)写出函数f(x)的最小正周期;
(2)试用“五点法”画出函数f(x)在区间
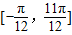 的简图,并指出该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
的简图,并指出该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?(3)若
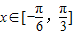 时,函数g(x)=f(x)+m的最小值为2,试求出函数g(x)的最大值并指出x取何值时,函数g(x)取得最大值.
时,函数g(x)=f(x)+m的最小值为2,试求出函数g(x)的最大值并指出x取何值时,函数g(x)取得最大值.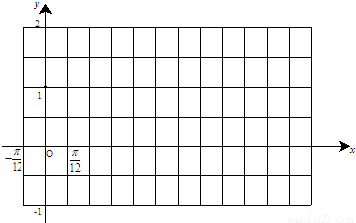
【答案】分析:(1)先利用向量数量积的坐标运算写出函数f(x)的解析式,再利用二倍角公式和两角和的正弦公式将函数化简为y=Asin(ωx+φ)的形式,最后由周期公式即可得f(x)的最小正周期
(2)由(1)f(x)=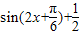 ,利用五点法,即将2x+
,利用五点法,即将2x+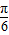 看成整体取正弦函数的五个关键点,通过列表、描点、连线画出函数图象,用图象变换的方法得此函数图象,可以先向左平移,再横向伸缩,再向上平移的顺序进行
看成整体取正弦函数的五个关键点,通过列表、描点、连线画出函数图象,用图象变换的方法得此函数图象,可以先向左平移,再横向伸缩,再向上平移的顺序进行
(3)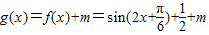 ,
,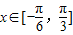 ,求此函数的最值可先将2x+
,求此函数的最值可先将2x+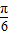 看成整体,求正弦函数的值域,最后利用函数g(x)=f(x)+m的最小值为2,解方程可得m的值,进而求出函数最大值
看成整体,求正弦函数的值域,最后利用函数g(x)=f(x)+m的最小值为2,解方程可得m的值,进而求出函数最大值
解答:解:(1)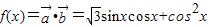 =
=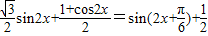
∴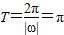
(2)
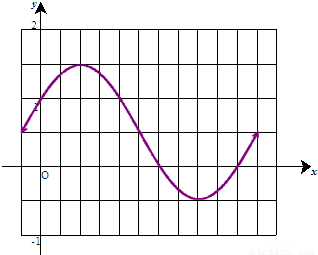
y=sinx向左平移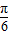 得到
得到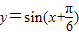 ,再保持纵坐标不变,横坐标缩短为原为的
,再保持纵坐标不变,横坐标缩短为原为的 变为
变为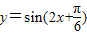 最后再向上平移
最后再向上平移 个单位得到
个单位得到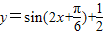
(3)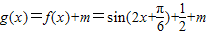 ,
,
∵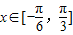 ,
,
∴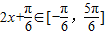
∴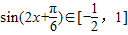 ,
,
∴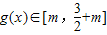 ,
,
∴m=2,
∴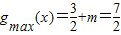
当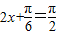 即
即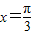 时g(x)最大,最大值为
时g(x)最大,最大值为 .
.
点评:本题综合考察了三角变换公式的运用,三角函数的图象画法,三角函数图象变换,及复合三角函数值域的求法.
(2)由(1)f(x)=
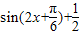 ,利用五点法,即将2x+
,利用五点法,即将2x+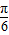 看成整体取正弦函数的五个关键点,通过列表、描点、连线画出函数图象,用图象变换的方法得此函数图象,可以先向左平移,再横向伸缩,再向上平移的顺序进行
看成整体取正弦函数的五个关键点,通过列表、描点、连线画出函数图象,用图象变换的方法得此函数图象,可以先向左平移,再横向伸缩,再向上平移的顺序进行(3)
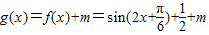 ,
,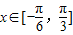 ,求此函数的最值可先将2x+
,求此函数的最值可先将2x+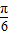 看成整体,求正弦函数的值域,最后利用函数g(x)=f(x)+m的最小值为2,解方程可得m的值,进而求出函数最大值
看成整体,求正弦函数的值域,最后利用函数g(x)=f(x)+m的最小值为2,解方程可得m的值,进而求出函数最大值解答:解:(1)
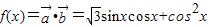 =
=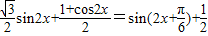
∴
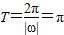
(2)
| x | 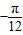 | 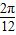 | 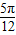 | 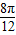 | 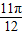 |
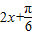 | 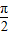 | π | 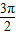 | 2π | |
sin(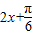 ) ) | 1 | -1 | |||
| y |  |  |  | 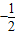 |  |

y=sinx向左平移
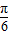 得到
得到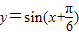 ,再保持纵坐标不变,横坐标缩短为原为的
,再保持纵坐标不变,横坐标缩短为原为的 变为
变为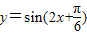 最后再向上平移
最后再向上平移 个单位得到
个单位得到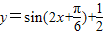
(3)
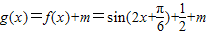 ,
,∵
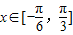 ,
,∴
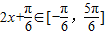
∴
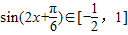 ,
,∴
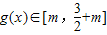 ,
,∴m=2,
∴
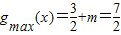
当
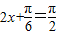 即
即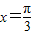 时g(x)最大,最大值为
时g(x)最大,最大值为 .
.点评:本题综合考察了三角变换公式的运用,三角函数的图象画法,三角函数图象变换,及复合三角函数值域的求法.

练习册系列答案
相关题目
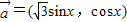 ,
,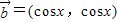 ,记
,记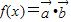 .
.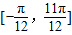 的简图,并指出该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
的简图,并指出该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?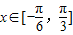 时,函数g(x)=f(x)+m的最小值为2,试求出函数g(x)的最大值并指出x取何值时,函数g(x)取得最大值.
时,函数g(x)=f(x)+m的最小值为2,试求出函数g(x)的最大值并指出x取何值时,函数g(x)取得最大值.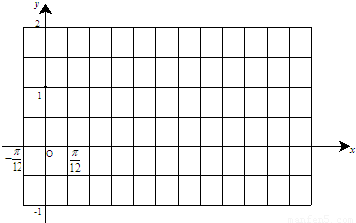
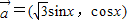 ,
,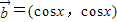 ,记
,记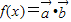 .
.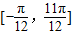 的简图,并指出该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
的简图,并指出该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?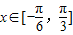 时,函数g(x)=f(x)+m的最小值为2,试求出函数g(x)的最大值并指出x取何值时,函数g(x)取得最大值.
时,函数g(x)=f(x)+m的最小值为2,试求出函数g(x)的最大值并指出x取何值时,函数g(x)取得最大值.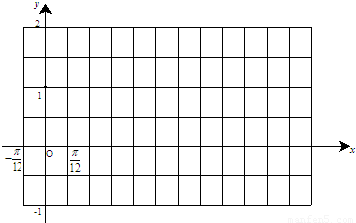
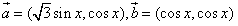 ,记
,记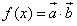 .
.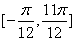 的简图,并指出该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
的简图,并指出该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?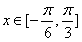 时,函数g(x)=f(x)+m的最小值为2,试求出函数g(x)的最大值并指出x取何值时,函数g(x)取得最大值。
时,函数g(x)=f(x)+m的最小值为2,试求出函数g(x)的最大值并指出x取何值时,函数g(x)取得最大值。 
 (3)若
(3)若