Question

 

已知函数f (x) = log_a x (a > 0且a≠1)，若数列：2，f (a₁)，f (a₂)，…，f (a_n)，2n + 4 (n∈N^﹡)为等差数列.

(1) 求数列{a_n}的通项公式a_n；

(2) 若a = 2，b_n = a_n·f (a_n)，求数列{b_n}前n项和S_n；

(3) 在(2)的条件下对任意的n∈N^﹡，都有b_n > f ^{- 1}(t)，求实数t的取值范围.

 

 

 

 

 

 

Answer 1

【答案】

 

解：(1) 由2n+4=2+(n+)d求得：d = 2，所以f (a_n)=2+(n+)·2 = 2n+2，求得：a_n=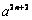.                                      (4分)

(2) b_n= a_n·f (a_n)= (2n+2)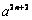=(n+1)·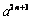 

S_n=2·2⁵+3·2⁷ +4·2⁹ +…+(n+1)·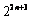, 错位相减得：

S_n= 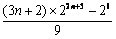                                   (8分)

    (3) ∵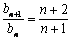·4 > 1，∴{ b_n }为递增数列. b_n中的最小项为：b₁=2·2⁵=2⁶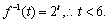，                      (14分)