题目内容
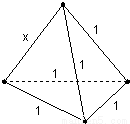
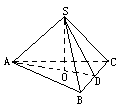
四面体的一条棱长是x,其它各条棱长都是1,(1)把四面体的体积V表示成x的函数f(x);(2)求f(x)的值域;(3)求f(x)的单调区间.
答案:
解析:
解析:
|
解:(1)如图,设BC=x,则S到面ABC的垂足O是△ABC的外心,连AO并延长交BC于D,则D是BC中点且AD⊥BC.易知AD=
(2)∵f(x)= (3)∵当x= |

练习册系列答案
相关题目
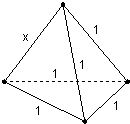 四面体的一条棱长为x,其余棱长均为1,体积为f(x),则函数y=f(x)在其定义域上( )
四面体的一条棱长为x,其余棱长均为1,体积为f(x),则函数y=f(x)在其定义域上( )| A、是增函数但无最大值 | B、是增函数且有最大值 | C、不是增函数且无最大值 | D、不是增函数但有最大值 |
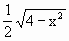 ,
,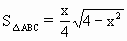 .设△ABC的外接圆半径为R,由R=
.设△ABC的外接圆半径为R,由R=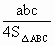 ,得R=
,得R=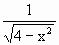 ,SO=
,SO=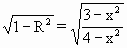 ,∴V=
,∴V=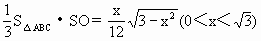 .
.
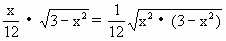 ,而
,而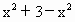 =3为定值,
=3为定值,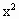 >0,3-
>0,3-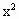 >0,∴当且仅当
>0,∴当且仅当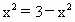 即
即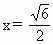 时,f(x)取得最大值
时,f(x)取得最大值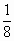 .∴f(x)的值域为
.∴f(x)的值域为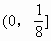 .
.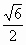 时,f(x)取得最大值.又∵0<x<
时,f(x)取得最大值.又∵0<x<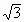 ,∴f(x)的递增区间是(0,
,∴f(x)的递增区间是(0,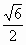 ],递减区间是[
],递减区间是[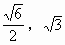 ).
).