题目内容
我们把由半椭圆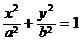 (x≥0)与半椭圆
(x≥0)与半椭圆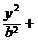
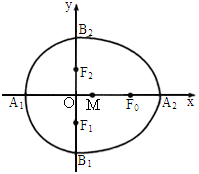
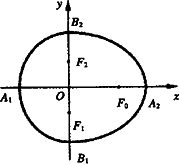
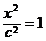 (x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0,如图,点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2分别是“果圆”与x 、y轴的交点
(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0,如图,点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2分别是“果圆”与x 、y轴的交点
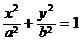 (x≥0)与半椭圆
(x≥0)与半椭圆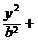
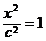 (x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0,如图,点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2分别是“果圆”与x 、y轴的交点
(x≤0)合成的曲线称作“果圆”,其中a2=b2+c2,a>0,b>c>0,如图,点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2分别是“果圆”与x 、y轴的交点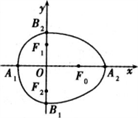
(1)若△FnF1F2是边长为1的等边三角形,求果圆的方程.
(2)当|A1A2|>|B1B2|时,求 的取值范围.
的取值范围.
(2)当|A1A2|>|B1B2|时,求
 的取值范围.
的取值范围.解:(1)由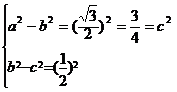 得
得
∴果圆的方程为
(2)a+c>2b,
∴a2-b2>(2b-a)2,
∴
又 b2>c2=a2-b2 ,

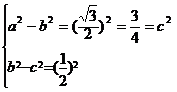 得
得
∴果圆的方程为

(2)a+c>2b,

∴a2-b2>(2b-a)2,
∴

又 b2>c2=a2-b2 ,


练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
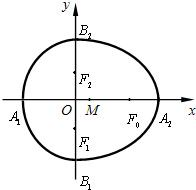 我们把由半椭圆
我们把由半椭圆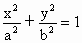 (x≥0)与半椭圆
(x≥0)与半椭圆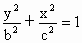 (x≤0)合成的曲线称作“果圆”,其中
(x≤0)合成的曲线称作“果圆”,其中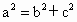 ,a>0,b>c>0.如下图,点
,a>0,b>c>0.如下图,点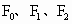 是相应椭圆的焦点,
是相应椭圆的焦点,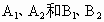 分别是“果圆”与x、y轴的交点.
分别是“果圆”与x、y轴的交点.
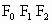 是边长为1的等边三角形,求“果圆”的方程;
是边长为1的等边三角形,求“果圆”的方程;
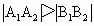 时,求
时,求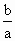 的取值范围;
的取值范围;