题目内容
已知f(x)=
，则f（2）+f（-2）的值为（ ）
|
分析：f(x)=
，f（2）=f（2-1）=f（1）=f（1-1）=f（0）=f（0-1）=f（-1）=（-1）2=1，f（-2）=（-2）2=4，由此能求出f（2）+f（-2）．
|
解答：解：∵f(x)=
，
∴f（2）=f（2-1）=f（1）=f（1-1）=f（0）=f（0-1）=f（-1）=（-1）2=1，
f（-2）=（-2）2=4，
∴f（2）+f（-2）=1+4=5．
故选B．
|
∴f（2）=f（2-1）=f（1）=f（1-1）=f（0）=f（0-1）=f（-1）=（-1）2=1，
f（-2）=（-2）2=4，
∴f（2）+f（-2）=1+4=5．
故选B．
点评：本题考查分段函数的解析式和求法，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
相关题目
(x)＝
；x＜0时，
R)，l(x)= 2x2+3x-1，h (x)为f (x)、g(x)在R上生成的一个二次函数.
，若h (x)为偶函数，求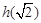
；
，若h (x)同时也是g(x)、l(x) 在R上生成的一个函数，求a+b的最小值；
R)，
=
2x2+3x-1，h (x)为f
(x)、g(x)在R上生成的一个二次函数.
，若h (x)为偶函数，求
；
，若h (x)同时也是g(x)、l(x) 在R上生成的一个函数，求a+b的最小值；